Intégrales
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Diabolik
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Fév 2006, 10:58
-
 par Diabolik » 07 Fév 2006, 09:53
par Diabolik » 07 Fév 2006, 09:53
Bonjour tout le monde, j'ai plusieurs intégrations à faire et 2 me causent des problèmes...
I= Int sin(x)^3 sur [0;Pi] avec le changement de variable cos(x)=u
Merci de votre aide.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Fév 2006, 10:59
par Nightmare » 07 Fév 2006, 10:59
Bonjour :happy3:
=sin(x).sin^{2}(x)=sin(x)(1-cos^{2}(x)))
=u\rightarrow du=-sin(x)dx)
ainsi :
(1-cos^2(x))=\Bigint -(1-u)du)
:happy3:
-
Diabolik
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Fév 2006, 10:58
-
 par Diabolik » 07 Fév 2006, 11:55
par Diabolik » 07 Fév 2006, 11:55
Je suis pas sur d'avoir compris comment tu arrives à la seconde intégrale...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Fév 2006, 12:09
par Nightmare » 07 Fév 2006, 12:09
euh oui, il manque un carré, erratum
-
Diabolik
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Fév 2006, 10:58
-
 par Diabolik » 07 Fév 2006, 13:42
par Diabolik » 07 Fév 2006, 13:42
Alors là je suis complètement perdu. Il manque un carré où?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 07 Fév 2006, 13:45
par Nightmare » 07 Fév 2006, 13:45
Bon
Tu as :
=u)
et donc
dx=1du)
(en dérivant)
Or j'ai montré que l'intégrale valait :
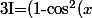)sin(x)dx)
donc avec le changement de variable :
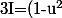\times (-1)du)
ie
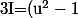du)
:happy3:
-
Diabolik
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Fév 2006, 10:58
-
 par Diabolik » 07 Fév 2006, 16:36
par Diabolik » 07 Fév 2006, 16:36
Yes, merci Nightmare.
Je trouve I=4/3, il me semble que c'est juste...
J'en ai encore une autre.
J=Int x.sin(x)^3 .dx sur [0;Pi]
Toujours avec un changement de variable (x=t-Pi) je dois trouver la relation entre Iet J.
Comment je dois faire?
-
isortoq
- Membre Naturel
- Messages: 73
- Enregistré le: 28 Jan 2006, 20:54
-
 par isortoq » 08 Fév 2006, 07:44
par isortoq » 08 Fév 2006, 07:44
Bonjour !
Je poserais plutôt x=pi-t, ce qui donne
J=Int (pi-t).(sin t)^3 .dt sur [0;Pi]
d'où J=pi.I-J et donc 2J=pi.I
-
Diabolik
- Membre Naturel
- Messages: 11
- Enregistré le: 03 Fév 2006, 10:58
-
 par Diabolik » 08 Fév 2006, 11:18
par Diabolik » 08 Fév 2006, 11:18
Ok, merci.
Si je me trompe pas le calcul d'une intégrale sur un intervalle donné correspond à la valeur de l'aire comprise entre l'axe des abscisses et la courbe.
Par exemple pour I je trouve 4/3. C'est l'air compris entre l'axe des abscisses et la courbe?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
