Intégrales et sommes...

[pouik]

Bonjour,
Pourriez-vous m'aider à traiter ces questions sur lesquelles je m'arrache les cheveux. Merci d'avance.

On note
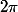
On note une fonction de vers , -périodique et de classe .
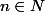
Pour tout , on note
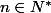
Pour tout , on note
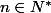
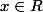
Pour tout et , on pose .

1. Montrer que, pour tout réel , on a :

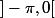
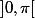
2. On fixe un réel . Montrer que la fonction , éfinie sur (union) par la relation , rest prolongeable en une fonction continue sur le segment .

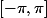
[tize]

Bonjour,
1) est très facile il suffit d'appliquer l'identité :
Pour la 2) n'oublie pas que est donc la limite en 0 de :
existe...

[pouik]

Bonjour,

Bonjour,
1) est très facile il suffit d'appliquer l'identité :
Pour la 2) n'oublie pas que est donc la limite en 0 de :
existe...

Mais à quoi dois-je appliquer la formule . désolé mais je ne vois pas ! :briques: :hum:

[tize]

et bien dans l'intégrale à :

[pouik]

D'accord, donc j'arrive à trouver que :

Mais je ne vois pas comment montrer que l'on a :
:marteau:

[pouik]

J'ai pensé à poser
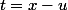
mais le problème c'est qu'avec ca on obtient :
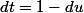
, ce qui pose quelques problèmes...

a moins que je ne me trompe. :hum:

[pouik]

Bonjour,
Pourriez-vous m'aider car je ne vois toujours pas comment montrer que :
Mais je ne vois pas comment montrer que l'on a :


Merci d'avance pour votre aide.

[tize]

Bon je t'ai déjà dit ce qu'il fallait faire :
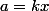
d'abord montrer que avec tu te sers de l'identité avec et .

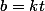
Ensuite montre que c'est un simple changement de variable

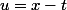
[pouik]

Bonjour,
non mais ca j'ai réussit à le faire, cf mon message de Hier 16h19

Bon je t'ai déjà dit ce qu'il fallait faire :
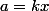
d'abord montrer que avec tu te sers de l'identité avec et .

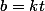
Mais c'est pour ca que j'ai du mal :

Ensuite montre que c'est un simple changement de variable

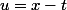
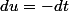
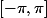
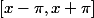
Avec ce changement de variable, on a : mais le problème c'est que lorsque décrit , décrit . A moins que je ne me trompes ?? :briques:

[tize]

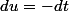
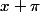
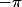
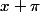
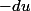
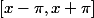
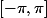
oui, et varie de à quand varie de à . En changeant le sens d'intégration varie alors de à et il faut ajouter un signe - devant l'intégrale qui va compenser le - du , on obtient alors : alors l'intégrale de qui est la même que l'intégrale de puisque l'intégrande est périodique.

[pouik]

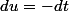
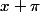
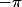
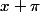
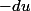
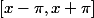
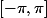
oui, et varie de à quand varie de à . En changeant le sens d'intégration varie alors de à et il faut ajouter un signe - devant l'intégrale qui va compenser le - du , on obtient alors : alors l'intégrale de qui est la même que l'intégrale de puisque l'intégrande est périodique.

Merci mais je ne comprends pas d'où vient le signe - qu'il faut ajouter devant l'intégrale... :hum: