Bonjours,
J'aimerais avoir votre aides pour simplifier des expressions avec des intégrales s'il-vous-plaît.
Voici l'exercice : https://ibb.co/0KFb0fw
Pouvez vous me donnez le résultats de la B et du C s'ils vous plait ? Merci
Intégrales simplification d'expression
4 messages
- Page 1 sur 1
Re: Intégrales simplification d'expression
par FSkyoss » 14 Avr 2020, 20:07
J'y arrive vraiment pas, y'a que la A que j'ai réussi.
Je dois le rendre pour demain donc pouvez vous me donnez le résultat de la B et C s'il-vous-plaît.
Je dois le rendre pour demain donc pouvez vous me donnez le résultat de la B et C s'il-vous-plaît.
Re: Intégrales simplification d'expression
par Carpate » 15 Avr 2020, 08:29
Bonjour,
C'est pourtant l'application immédiate des formules déjà données :
}dx -\int_0^{-2}\frac{1}{(1+x^2)}dx=\int_0^1\frac{1}{(1+x^2)}dx +\int_{-2}^0\frac{1}{(1+x^2)}dx=\int_{-2}^0\frac{1}{(1+x^2)}dx +\int_0^1\frac{1}{(1+x^2)}dx)
}dx)
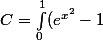dx+\int_0^11.dx+\int_0^1e^{x^2}dx=\int_0^1(e^{x^2}-1+1+e^{x^2})dx = ...)
C'est vraiment au niveau "Supérieur" ?
C'est pourtant l'application immédiate des formules déjà données :
C'est vraiment au niveau "Supérieur" ?
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :