Intégrales et études de fonctions

[Anonyme]

Ah je viens de remarquer ! Pourquoi est-ce que ce serait faux ? Tu pourrais me donner plus d'explications ?

@Kikoo <3 Bieber

f(x)=1/x n'est pas une application de IR dans IR

ps)
N'importe quelle fonction de E dans F
qui pour un élément de l'ensemble de départ : E n'a pas d'image dans F
fait que la fonction f n'est pas une application de E dans F

[Kikoo <3 Bieber]

Non non, 1/x n'est pas définie sur R en effet, mais qu'est-ce qui l'empèche d'avoir le "statut" d'application ?
Elle est bien application de R* dans R*

[ThekamikazeFou]

hum, il parlait d'application en expliquant que chaques fonctions ont un intérêt physique, chimique, mécanique, électrique etc. il me semble non?

[Anonyme]

@Kikoo <3 Bieber

Je répète ce que j'essaie de t'expliquer :

N'importe quelle fonction de E dans F
qui pour un élément de l'ensemble de départ : E n'a pas d'image dans F
fait que la fonction f n'est pas une application de E dans F

Autre exemple :
la fonction f(x)=x "définie" sur IR+ n'est pas une application de IR dans IR

ps)
j'espère que tu comprends pourquoi j'ai écrit "définie"

car on doit écrire la fonction f définie par f(x)=x si x appartient à IR+

[Kikoo <3 Bieber]

hum, il parlait d'application en expliquant que chaques fonctions ont un intérêt physique, chimique, mécanique, électrique etc. il me semble non?

Je ne vois pas le lien non :hein:

Ce que je veux dire, c'est que mathématiquement parlant, une fonction est une application mais la réciproque n'est pas vraie. La distinction entre ces deux notions peut être discutable et est désormais un peu floue, dans le sens où il n'y a pas de norme véritablement admise pour parler d'application ou de fonction.

[Anonyme]

@Kikoo <3 Biebe et @ThekamikazeFou]

OK

Question :
Pouvez vous écrire un exemple d'une fonction réelle à 1 variable réelle qui n'est pas une application ?

[ThekamikazeFou]

(x²+1)² dans R- ?

[Anonyme]

(x²+1)² dans R- ?

Bof bof ...

Est ce que tu "parles" de la fonction définie par

:


?

si oui alors c'est Bof bof bof ET bof

ps)
Moi je dis que cette fonction est une application de IR- dans IR
car tout x de IR- (ensemble de départ) il existe un y dans IR ( ensemble d'arrivée) tel que f(x)=y

[ThekamikazeFou]

Bof bof bof ET bof

Est ce que tu parles de la fonction définie par

:



ps)
Moi je dis que cette fonction est une application de IR- dans IR
car tout x de IR- (ensemble de départ) il existe un y dans IR ( ensemble d'arrivée) tel que f(x)=y

C'est une application de R- dans R ou de R+ dans R non?

[Anonyme]

@ThekamikazeFou

1) c'est une application de R- dans R

2) c'est une application de R+ dans R (ou dans R+)

3) c'est une application de R dans R (ou dans R+)

4) c'est n'est pas une bijection de R dans R (ou dans R+)

ps)
Tu aurais pu prendre la fonction carré ?
Pourquoi chercher un truc comme

[Kikoo <3 Bieber]

Oulah on ne parle plus d'application mais de complication ! (blague à deux balles ouais je sais)

[Rockleader]

Moi je dirais une fonction du genre

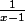
pour x = 1, on n'a pas d'image puisque c’est une valeur interdite, donc si je suis ton raisonnement, pas d'image donc ce n'est pas une application.

[Anonyme]

@Rockleader
YES, you are right !

[Rockleader]

@Rockleader
YES, you are right !

Ok, donc je suis le seul qui avait rien compris au début et qui trouve la solution

[Anonyme]

@Rockleader

On parle d'application

qui est une notion qui ne sert pas à grand chose
avec les fonctions réelles
si on travaille sur le domaine de définition "de la dite fonction"

[Kikoo <3 Bieber]

Ok, donc je suis le seul qui avait rien compris au début et qui trouve la solution

Tu apprends vite, c'est bien =)

Par contre, je suis toujours pas vraiment d'accord avec Ptitnoir en ce qui concerne les applications et les fonctions.
D'après moi, une fonction est certainement une application si l'on considère des ensembles adaptés. Par contre, une application n'est pas forcément une fonction...

[Anonyme]

Par contre, une application n'est pas forcément une fonction...

NON Faux
car une "application" est une fonction particulière !
au même TITRE que "une bijection" est une fonction particulière (et dans ce cas et seulement dans ce cas il existe une fonction réciproque)

[Kikoo <3 Bieber]

Hmmm... mouais, je suis pas vraiment convaincu :) J'ai toujours pensé une fonction comme étant une application particulière.

[Anonyme]

Hmmm... mouais, je suis pas vraiment convaincu J'ai toujours pensé une fonction comme étant une application particulière.

Comme tu es philosophe , tu vas réfléchir.... et tu pourras toi même conclure sur cette interrogation...

[Kikoo <3 Bieber]

Ah non, réfléchir au sens de "application" et "fonction" c'est réfléchir au sens que les matheux ont voulu donner à ces deux notions, et non pas à la définition intrinsèque de ces choses-là (parce que de toute façon, l'Homme a inventé les maths, et ne les a pas découvertes).