Intégrales et études de fonctions

[Rockleader]

Bonsoir, j'essaie de faire un sujet d'entrainement


Soit f(x) = arctan(sin(x))

1-

Faire une étude complète de la fonction f : ensemble de de;)nition Df , continuité, dérivabilité,
calcul de f'(x), tableau de variation et graphe.

2- DOnner le plus grand intervalle I contenant [0;1] tel que f soit une bijection de I dans J = f(I). Justifier votre choix et expliciter J.
Calculer g'(y) pour tout y appartenant à J où g est la fonction réciproque de f.

3-
Montrer que arctan(x) >= x-(x^3)/3 pour tout x appartenant à [0;1], que sin(x)<=x pour x >=0, et que sin(x) >= x-(x^3)/6 pour x >=0.
En déduire que f(x) >= x-(x^3)/2 pour x appartenant à [0;1] et donner le nombre de solution de l'équation f(x)=1/2 dans l'intervalle [0;1]

1- Df = R
Pour la continuité, y a t'il une méthode à employer ? J'ai envie de dire que l'on a pas de valeurs interdites puisque pas de dénominateur.
La dérivabilité, je connais la définition, mais c'est en un point et non sur un intervalle, donc je sais pas trop comment adapter...
f' ça ne devrait pas poser trop de soucis simple fonction composé, de même que le tableau de variation.
Pour le graphe, est ce qu'il y a une méthode particulière pour la construction ? Parce qu'à partir du moment ou on a le tableau ya rien de bien compliquer à faire...

2-

J'ai toujours du mal à comprendre les histoires de bijection j'aurais besoin d'un coup de main là aussi^^

f(x) = arctan(sin(x))
Donc g(arctan(sin(x))) = x si j'ai bien saisi la définition. Mais ça ne me dis pas comment trouver g pour autant.

et 3 ben je verrais après --'

[ThekamikazeFou]

Qu'est ce que tu ne comprends pas dans la bijection?!
Par exemple arctan x est une bijection de R dans ]-PI/2,PI/2[
A l'inverse tan x est une bijection de ]-PI/2,PI/2[ dans R
De maniere génerale quelques soit x et quelque soit y on a y =tanx <=> x = Arctan y

Cela s'explique aussi par la formule tan(Arctanx) = x attention, Arctan(tan O) = O (ici il s'agit d'un angle)

D'apres toi qu'elle est la reciproque de f ? En fait il s'agit de f^-1 .
Qu'elle est la derivée de Arctan x ?


Si c'est le terme bijection qui te derangé, il signifie que pour un interval I il existe une image J de cet interval.
C'est a dire pour tout x appartenant a I il existe une unique solution dans J tel que f(I)=J

[Anonyme]

J'ai toujours du mal à comprendre les histoires de bijection j'aurais besoin d'un coup de main là aussi

Salut

Soit la fonction "carré" : c'est à dire
la fonction définie par quand

1) car

2) La fonction n'est pas une bijection de sur car le nombre (c'est un exemple) a DEUX antécédents qui sont et

3) Soit la fonction qui est la restriction de la fonction "carré" sur
c'est à dire la fonction définie par si

Cette fonction est une bijection (ou une fonction bijective) de sur
car tout élément de l'ensemble d'arrivée n'a qu'UN SEUL antécédent dans l'ensemble de départ

En conclusion :
Comme cette fonction est une fonction bijective de sur
on peut définir une fonction réciproque , notée
et qui est définie par si

ET on a
et

c'est à dire

J'espère que cela va t'aider à comprendre un peu plus les histoires de [I]"fonctions bijectives"....[/I]

ps)
Autres notions/mots en rapport avec ce sujet
- une fonction qui est une "application" d'un ensemble dans/sur un ensemble
- une fonction qui est "injective" d'un ensemble dans/sur un ensemble
- une fonction qui est "surjective" d'un ensemble dans/sur un ensemble

[Rockleader]

Si j'ai bien compris pour ma fonction, le plus grand intervalle contenant [0;1] est -oo;+oo puisque ma fonction est continue il y aura une image pour tout x

[Anonyme]

@Rockleader

La fonction f définie par f(x) = arctan(sin(x)) est bijective de I sur J
si et seulement si
la fonction sinus est bijective de I sur K et la fonction arctangtente est bijective de sin(K) sur J

[Rockleader]

@Rockleader

La fonction f définie par f(x) = arctan(sin(x)) est bijective de I sur J
si et seulement si
la fonction sinus est bijective de I sur K et la fonction arctangtente est bijective de sin(K) sur J

Ok, mais tout ça c'est de la théorie, si je conçois à peu près ce qu'on dis, j'arrive pas à voir ce que ça donne concrètement avec les valeurs.

Si j'ai bien compris ici K est une valeur et I est un intervalle mais je vois pas bien la façon dont on peut lier les deux de manière concrète avec les valeurs et non théoriquement.

Ce qu'il me faudrait c'est un exemple numérique concret sur une fonction quelconque.

[ThekamikazeFou]

Tu veux un exemple concret? Très bien;
On a une fonction f(x) = (3x+4)/x-1
A premiere vu on pourrait croire que f est une bijection de R dans R, verifions cela.
X dois etre different de 1 donc on peut penser que f est une bijection de R\{1} dans R
Verifions de nouveau.
Par definition nous avons actuelement pour tout x different de 1 une image et une seul dans R. C'est a dire, quelque soit y appartenant R on a un unique antécédent x appartenant a R\{1}
Mais resolvns Y= (3x+4)/(x-1)
Donc on a x = (y+4)/(y-3) si et seulement si y est different de 3
Donc pour tout y appartenant a R\{3} f admet un unique antécédent.

On comprend alors que f est une bijection de R\{1} dans R\{3}
Et cela semble logique. Si la fonction f n'est pas defini pour une valeur x0 cela signifie que sur R la valeur f(x0) n'existe pas

As tu compris?!

[Rockleader]

Je pense avoir compris merci.

Pour en revenir à mon exercice donc, sin est défini sur R. et arctan aussi. Donc la bijection est de R sur R normalement.



Si ce n'est pas ça, j'aimerais aussi un exemple par exemple pour f(x)=3x+4

ici x est défini pour tout R donc il n'y a pas de raisons pour que ce soit différent pour y non ?

[Anonyme]

@Rockleader

1) Trace la fonction sinus sur ta calculatrice

2) et essaie de voir pourquoi ce n'est pas une fonction bijective de IR sur [-1 , 1]

3) puis essaie de trouver le plus grand intervalle I de IR tel [0 , 1] I
et tel que la fonction sinus est une fonction bijective de I sur [-1 , 1]

[ThekamikazeFou]

J'espere repondre à t'as question,
F(x)= 3x+4 est une bijection de R dans R. Pour n'importe qu'elle valeur de X on aura une image Y

C'est la meme chose pour ta fonction Arctan(Sin(x))
Ici g(y) est la reciproque.
F est une bijection de I dans J donc g(y) est une bijection de J dans I
Les intervalles sont inversé puisqu'il s'agit de la fonction reciproque.
Par exemple tan(x) est une bijection de quoi dans quoi? Et sa reciproque Arctan(x) ?

[Rockleader]

@Rockleader

1) Trace la fonction sinus sur ta calculatrice

2) et essaie de voir pourquoi ce n'est pas une fonction bijective de IR sur [-1 , 1]

3) puis essaie de trouver le plus grand intervalle I de IR tel [0 , 1] I
et tel que la fonction sinus est une fonction bijective de I sur [-1 , 1]

Je l'ai tracé, et le sinus est bien défini sur R car pour tout x de R sinus(x) est compris dans [-1;1] J'aurais plutot tendance à dire donc que c'ets une fonction bijective de R sur [-1;1]....

[Anonyme]

Je l'ai tracé, et le sinus est bien défini sur R car pour tout x de R sinus(x) est compris dans [-1;1] J'aurais plutot tendance à dire donc que c'ets une fonction bijective de R sur [-1;1]....

NON

Il suffit de résoudre l'équation : (c'est un exemple)

ET cette équation a une "une infinité" de solutions (car la fonction sinus est périodique)
Cela veut dire que le nombre a une infinité (donc plusieurs) antécédents...

ET DONC cela veut dire que la fonction sinus n'est pas bijective de IR sur [-1 , 1]

ps)
L'intervalle que tu recherches dans ton exo est :

Essaie de comprendre pourquoi et de le justifier correctement par un raisonnement ou une explication mathématique

Conseil :
Etudie la fonction définie par

EDIT
et démontre que est une bijection de IR sur

[Rockleader]

Ah, il faut donc qu'il n'y est qu'un seul antécédent pour qu'il y est bijection.

Si l'intervalle I est bien celui là c'est parce que c'est le plus grand intervalle entre sin et arctan.

arctan qui est défini sur -pi/2 ; pi/2 est un intervalle supérieur à -1;1

J'aurais pourtant dis que ça aurait été le plus petit...

[Anonyme]

Ah, il faut donc qu'il n'y est qu'un seul antécédent pour qu'il y est bijection

Conseil :
Relis les différents messages dans cette discussion (ou ton cours)
car il faut avant de faire ton exo comprendre ce qu'est une bijection de I sur J ...

Il est tard et je crois qu'il est temps d'aller faire dodo....

[Anonyme]

@Rockleader

Salut

Comme je vois que tu as ouvert d'autres discussions sur Maths-Forum sur d'autres sujets ( notamment sur les primitives car tu dois étudier en ce moment les primitives et les intégrales )

est-ce-que ce sujet est clos et que tu as compris ce qu'est une bijection ?

Pour information : (avant de clore cette discussion )

Sais tu que si la fonction est une bijection dérivable ,
ALORS sous certaines conditions
la fonction est également dérivable ?

ET il existe une formule importante permettant de calculer la fonction dérivée de


ps)
Si tu as oublié ou si tu ne sais pas je te conseille de noter quelque part cette formule
(qui est écrite et expliquée dans ton cours ou dans ton livre de maths)

[Rockleader]

Non, j'ai toujours du mal avec les bijections c'est un des points du controle que je pense avoir loupé...

[Anonyme]

Non, j'ai toujours du mal avec les bijections c'est un des points du controle que je pense avoir loupé...

Salut
Et bien relis tous mes messages car j'ai fait un effort pour essayer d'expliquer le plus simplement possible cette notion en t'expliquant "tout" ce qu'il vaut savoir sur ce sujet.

Et si tu ne comprends pas quelque chose dans mes explications,
n'hésite pas à poser des questions

[Anonyme]

@Rockleader

Ce message est juste pour te donner un dernier coup de pouce qui "devrait" (théoriquement) t'aider à comprendre cet exo
et notamment cette "étrange fonction" qui est

1) As tu tracé cette fonction sur ta calculatrice ?
Si tu l'as fait , voici ce que tu as "vu"


2) Si tu "analyses" la courbe , tu peux "voir un "paquet de propriétés" de la fonction :

2.1) La fonction est définie sur , elle est continue et dérivable , elle est périodique

2.2) Pour tout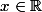 on a :

2.3) La fonction n'est pas une bijection de sur

2.4) La restriction de la fonction à l'intervalle EST UNE BIJECTION de sur

En conclusion :
Ce que j'essaie de t'expliquer , en écrivant ce message , c'est que à partir de la classe de Terminale ,
il faut commencer à apprendre à analyser "ce qu'on voit"
( et notamment les représentations graphiques de fonction que tu peux très facilement afficher sur ta calculatrice graphique )

En espérant que ce message va faire un GROS TILT dans ta tête et que tu vas tout comprendre

A+

ps)
Une fois que tu as "vu tout cela" , les calculs de la bijection réciproque et de sa fonction dérivée sont uniquement des calculs !

De plus tu as plein d'exemples dans ton cours ou bouquin de maths sur comment faire ces calculs

[Rockleader]

Ben en fait ce que je comprends pas en réalité c'est le terme de bijection et seulement le terme, quelle définition on donnerait au mot bijection sans parler nécessairement de math. Parce qu'après je comprends plus ou moins ce que tu écris mais ça reste de l'à peu près...du moins dans ma tête^^

[Anonyme]

@Rockleader

Une bijection est une propriété d'une fonction

Soit f est une fonction d'un ensemble E vers un ensemble F

f est une bijection de E sur F
si tout élément de F a un est un seul ANTECEDENT dans E
et si F=f(E)


Si tu ne comprends toujours pas , je te conseille
-soit de prendre des exemples simples
- soit de faire des dessins avec des "patates" pour "dessiner" les ensembles E et F
-soit de relire le message dans cette discussion qui explique pourquoi f(x)=x^2 n'est pas une bijection de IR sur IR+
-soit relire ton cours et ton livre de maths sur ce sujet (si tu as eu un cours sur ce sujet ?)
-soit de prendre un cours particulier avec un prof de maths sur cette notion
( je dis cela car visiblement , tu bloques sur quelque chose , mais je ne sais pas quoi ? )

ps1)
En classe de terminale , les élèves étudient "le théorème de la bijection" sans trop savoir ce qu'est une bijection

Et la plupart des élèves en classe de terminale pensent qu'une bijection est une fonction continue strictement monotone (et c'est déjà pas mal de comprendre cela)


ps2)
Sur ce , j'arrête d'intervenir dans cette discussion car je ne suis pas là pour t'embêter
Je ne sens pas de ta part une motivation quelconque à travailler ce sujet

donc A+ dans d'autres discussions sur Maths-Forum