Integrale d'une fonction

[Doraki]

Parce que P1(C) est de dimension 2 donc tu ne peux qu'intégrer des 2-formes différentielles dessus. Or ton 1/z dz, au mieux c'est une 1-forme différentielle. Donc ça n'a vraiment aucun sens de vouloir intégrer ça et d'obtenir un nombre à la fin.

[barbu23]

Parce que P1(C) est de dimension 2 donc tu ne peux qu'intégrer des 2-formes différentielles dessus. Or ton 1/z dz, au mieux c'est une 1-forme différentielle. Donc ça n'a vraiment aucun sens de vouloir intégrer ça et d'obtenir un nombre à la fin.

A ma connaissance : est une "droite" : c'est la droite projectif. Et une droite est un objet de dimension , non ?
Un coup d'oeil par ici : http://fr.wikipedia.org/wiki/Droite_projective ou par là : http://fr.wikipedia.org/wiki/Sph%C3%A8re_de_Riemann
est isomorphe à un cercle complexe ( sphère de Riemann ), et un cercle est un truc de dimension , non ?
Merci d'avance. :happy3:

[barbu23]

Si on munit localement chaque carte de d'une métrique convenable ( la valeur absolue locale sur ), peux -t-on définir la notion de bornitude dans ?
Pour vous orienter un peu plus par rapport à l'idée que je cherche à vous transmettre, veuillez jeter un oeil sur le pdf qui se trouve sur le lien suivant : http://www.maths-forum.com/showthread.php?t=156499&highlight=spectre à la page : , paragraphe :
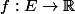Vous allez comprendre comment la notion de séparation a été retranscrite en théorie des schémas, et par quel moyen elle a été retranscrite, alors qu'il s'agit d'une notion purement topologique. La même philosophie peut se transmettre à cette notion de bornitude topologique dans le cas des variétés à travers la propriété : est compact et est localement bornée, implique que est bornée.
Il reste à savoir la méthode de calcul du supremum de qui n'est pas du tout claire.
Avez vous des suggestions ?

Merci d'avance. :happy3:

Edit :
Voici ce que j'ai suggéré dans un post précédent :

ça veut dire à mon avis que :
avec : sont respectivement des cartes locales de , non ?.
C'est juste une "expectation", ce n'est pas absolue. Je réfléchis encore à ce que ça pourrait être cette notion de bornitude sur . :happy3:
Et toi, tu peux deviner qu'est ce que c'est ?

Êtes vous d'accord avec ? sinon, pourquoi ?

Merci d'avance.

Edit : Ce qui me laisse penser que notre est bornée, c'est la propriété qui dit que si est continue sur un compact, alors elle est bornée et atteint ces bornes. et donc, est intégrable.

[SLA]

Attends tu nous dis que le sujet bornitude n'est pas important (en gros parce que tu ne sais pas m'expliquer) puis tu le remets sur le tapis!
Par ailleurs une fonction bornée (même sur un compact) n'est pas forcément intégrable.
Bref explique nous avec quoi tu travailles?

[barbu23]

Attends tu nous dis que le sujet bornitude n'est pas important (en gros parce que tu ne sais pas m'expliquer) puis tu le remets sur le tapis!
Par ailleurs une fonction bornée (même sur un compact) n'est pas forcément intégrable.
Bref explique nous avec quoi tu travailles?

Non, je n'ai pas dit que le sujet de bornitude n'est pas important, j'ai dit que je ne suis pas en ce moment prêt à t'expliquer ce qu'est la notion de métrisabilité d'une topologie. ( Il me faut réviser le cours ).
Une fonction bornée sur un compact n'est pas forcément intégrable. Tu peux me donner un exemple ? Moi, j'ai dit, une fonction continue sur un compact est intégrable.
Je n'ai pas compris ta dernière question.
Si tu n'a pas le premier chapitre du livre que je suis entrain de feuilleter, je ne suis pas sûr de comprendre de quoi je parle. Le livre s'intitule : Riemann Surfaces. L'uteur du livre s'appelle : Otto Forster. Mais, sur ce livre, on ne parle pas du tout de la notion de l'integrale de fonction sur des surfaces de Riemann. Mais, avant de se lancer dans ces prétendus integrales, il faut avoir une petite idée sur la manière d'étudier ces fonctions. C'est important. Et ainsi, on peut avancer rapidement dans cette discussion il me semble.

Merci d'avance pour votre aide.

[SLA]

Non, je n'ai pas dit que le sujet de bornitude n'est pas important, j'ai dit que je ne suis pas en ce moment prêt à t'expliquer ce qu'est la notion de métrisabilité d'une topologie. ( Il me faut réviser le cours ).
Une fonction bornée sur un compact n'est pas forcément intégrable. Tu peux me donner un exemple ? Moi, j'ai dit, une fonction continue sur un compact est intégrable.
Je n'ai pas compris ta dernière question.
Si tu n'a pas le premier chapitre du livre que je suis entrain de feuilleter, je ne suis pas sûr de comprendre de quoi je parle. Le livre s'intitule : Riemann Surfaces. L'uteur du livre s'appelle : Otto Forster. Mais, sur ce livre, on ne parle pas du tout de la notion de l'integrale de fonction sur des surfaces de Riemann. Mais, avant de se lancer dans ces prétendus integrales, il faut avoir une petite idée sur la manière d'étudier ces fonctions. C'est important. Et ainsi, on peut avancer rapidement dans cette discussion il me semble.

Merci d'avance pour votre aide.

Beh la constante 1 sur [0,1] avec la mesure dx/x !
Sache qu'avant d'aller plus loin, il existe aussi des fonctions non bornées mais integrables.
Si tu veux parler bornitude il faut une metrique. Tu nous as dit que P1 est métrisable. Donne nous donc cette métrique!
Ensuite avant de parler d'integrale il faut une mesure. Donc quelle tribu? Quelle mesure?
Et je le dis tout de suite: personne ne répondra a cette question a ta place!
Cordialement

[barbu23]

D'accord, une petit question apparemment stupide. Est ce que : 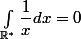avec 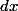la mesure de Riemann ? J'ai oublié les méthodes de calcul que nous utilisons en intégrales impropres. J'ai tendance à dire que l'intégrale vaut , car c'est une fonction impaire, mais puisqu'il s'agit d'une intégrale impropre, je me dit que le zéro qui est un point singulier peut nous réserver des surprises.
Merci d'avance.

[SLA]

D'accord, une petit question apparemment stupide. Est ce que : avec la mesure de Riemann ? J'ai oublié les méthodes de calcul que nous utilisons en intégrales impropres. J'ai tendance à dire que l'intégrale vaut , car c'est une fonction impaire, mais puisqu'il s'agit d'une intégrale impropre, je me dit que le zéro qui est un point singulier peut nous réserver des surprises.
Merci d'avance.

Ce n'est pas une intégrale de Riemann, même généralisée.

Édit: et encore je traduis. Parce que je ne sais pas ce que tu entends par mesure de Riemann...

[barbu23]

Tu nous as dit que P1 est métrisable. Donne nous donc cette métrique!
Ensuite avant de parler d'integrale il faut une mesure. Donc quelle tribu? Quelle mesure?
Cordialement

est métrisable par définition d'une variété. Et, je ne comprends pas ce que ça veut dire. :hum:

[vingtdieux]

Pour la première intégrale voir la valeur principale de Cauchy.

[barbu23]

Pour la première intégrale voir la valeur principale de Cauchy.

Peux tu étayer tes propos stp où m'indiquer un lien sur le net portant sur la valeur principale de Cauchy ?
La avleur principale de Cauchy, je l'ai apprises dans le cours des distributions de Frédéric Golse, disponible gratuitement sur le net ... je ne sais pas si tu fais allusion à cela.
Merci d'avance. :happy3:

[SLA]

Peux tu étayer tes propos stp où m'indiquer un lien sur le net portant sur la valeur principale de Cauchy ?
La avleur principale de Cauchy, je l'ai apprises dans le cours des distributions de Frédéric Golse, disponible gratuitement sur le net ... je ne sais pas si tu fais allusion à cela.
Merci d'avance. :happy3:

C'est la manière la plus simple d"attribuer une intégrable (finie) à 1/x. Et c'est exactement le même fonctionnement que pour en faire une distribution, donc oui il parle bien de ça.

[barbu23]

C'est la manière la plus simple d"attribuer une intégrable (finie) à 1/x. Et c'est exactement le même fonctionnement que pour en faire une distribution, donc oui il parle bien de ça.

Merci, il n'y'a pas de méthodes directes ( utilisé par les étudiants en L2 ) pour calculer : ? Je suis nul en intégrales impropres pour être claire.

Merci d'avance.

[SLA]

est métrisable par définition d'une variété. Et, je ne comprends pas ce que ça veut dire. :hum:

Je viens de feuilleter ton bouquin. Il n'est nullement question de métrique (en particulier) pour P1

[SLA]

est métrisable par définition d'une variété. Et, je ne comprends pas ce que ça veut dire. :hum:

Je viens de feuilleter ton bouquin. Il n'est nullement question de métrique (en particulier) pour P1...

[barbu23]

Je viens de feuilleter ton bouquin. Il n'est nullement question de métrique (en particulier) pour P1

Et il est question de quoi alors ?
Tu regardes à la page et ici : http://www.math.u-psud.fr/~paulin/notescours/cours_geodiff.pdf
Toute variété est un espace topologique métrisable.
Qu'est ce que ça veut dire ? Qu'elle est plutôt métrisable localement sur des cartes ? métrisabilité sur un espace non plat où la courbure fait apparition, ça n'a pas de sens. C'est le cas des variétés généralement.
Normalement, sur des espaces courbés, on ne munit pas l'espace de métrique, mais on muni son fibré de métrique, c'est le cas de la géométrie Riemannienne. Bref, une variété métrisable n'a aucun sens à mon avis. Métrisable veut dire métrisable sur son fibré. Donc, il faut préciser ce qu'on entend par métrisable. Qu'est ce que ça veut dire ?

[SLA]

Et il est question de quoi alors ?

On le munit d'une topologie. Et comme je l'ai déjà dit plein de fois: jamais on ne va chercher une métrique qui engendre sa topologie.

Tu regardes à la page et ici : http://www.math.u-psud.fr/~paulin/notescours/cours_geodiff.pdf
Toute variété est un espace topologique métrisable.
Qu'est ce que ça veut dire ?

Ben écoute. Il y a une définition précise d'espace topologique métrisable.

Qu'elle est plutôt métrisable localement sur des cartes ?

Tu ne sais même pas ce qu'est un espace métrisable, alors localement métrisable, ça veut dire quoi pour toi?

métrisabilité sur un espace non plat où la courbure fait apparition, ça n'a pas de sens.

N'importe quoi! on sait parfaitement mettre des métriques sur le cercle!

C'est le cas des variétés généralement.
Normalement, sur des espaces courbés, on ne munit pas l'espace de métrique,

C'est ce que je dis depuis le début. Mais c'est toi qui parle de fonction bornée à valeur dans P^1.

mais on muni son fibré de métrique, c'est le cas de la géométrie Riemannienne. Bref, une variété métrisable n'a aucun sens à mon avis.

Exactement le contraire de ce que tu cites du poly...

Métrisable veut dire métrisable sur son fibré.

non.

Donc, il faut préciser ce qu'on entend par métrisable. Qu'est ce que ça veut dire ?

As-tu seulement fait une recherche?

[barbu23]

Moi, je t'ai tout déversé devant toi, et j'ai précisé ce qui me rebute en détail, mais, toi, tu ne veux pas m'aider du tout. C'est quoi métrisable ?. :happy3:
Quelle est la métrique que tu mets sur un cercle ?

[SLA]

Moi, je t'ai tout déversé devant toi, et j'ai précisé ce qui me rebute en détail, mais, toi, tu ne veux pas m'aider du tout. C'est quoi métrisable ?. :happy3:
Quelle est la métrique que tu mets sur un cercle ?

Tu rigoles? J'ai écris plusieurs fois dans ce fil ce que veux dire métrisable.
N'importe qu'elle métrique de R^2, induite sur le cercle te donne une métrique sur le cercle.
Et même plus malin, dans le cas de la sphère centrée en l'origine (pour simplifier les calculs) avec u.v le produit scalaire et |u| la norme euclidienne.

[vingtdieux]

Pour info: On utilise x vp 1/x en théorie des distributions et on montre que la distribution vaut 1. On se sert pour cela de la vp de Cauchy définie en mathématiques "classiques" et de la définition des distributions régulières (intégrales de fonctions)