Integrale d'une fonction continue !

par **barbu23** » 19 Aoû 2007, 18:26

Bonjour :
Soit

une fonction definie sur

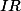
par :

.

peut s'ecrire de la manière suivante :

.
Alors : pour

:

.
Par contre, si on calcule l'integrale de

qui est egale à

, on obtient un resultat different du premier :
En effet :

.

par **barbu23** » 19 Aoû 2007, 18:28

On ne peut intervertir l'integrale et la somme que s'il y'a convergence uniforme n'est ce pas !!
Je vois maintenant pourquoi ça marche pas !!
Merci quant même à vous tous !!

par **achille** » 19 Aoû 2007, 18:40

salut, pour la notation 1{x} ça veut dire ? juste pour pouvoir suivre...

par **kazeriahm** » 19 Aoû 2007, 18:53

c'est la fonction caractéristique de {x}

si E est un ensemble alors 1_E est la fonction définie par x->1 si x est dans E, 0 sinon

par **quinto** » 19 Aoû 2007, 19:20

Bonjour,
déjà je ne vois pas ce que signifie

par **quinto** » 19 Aoû 2007, 19:21

barbu23 a écrit:On ne peut intervertir l'integrale et la somme que s'il y'a convergence uniforme n'est ce pas !!

Il y'a plein d'exemples où on peut intervertir les deux mais où il n'y a pas convergence uniforme.

par **barbu23** » 19 Aoû 2007, 20:24

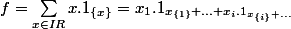
avec :

ça n'existe pas ?!

par **achille** » 19 Aoû 2007, 20:25

l'écriture en sigma ne sera autre que x, si 1{x} est la fonction caractéristique de {x}.

par **barbu23** » 19 Aoû 2007, 20:26

oui c'est la fonction caracteristique !!

par **barbu23** » 19 Aoû 2007, 21:30

Est ce qu'on a droit d'intervertir ou non dans cet exemple là ?
Merci d'avance !!

par **barbu23** » 19 Aoû 2007, 22:22

:chef: :help: :lol5:

par **fahr451** » 19 Aoû 2007, 22:25

je ne comprends pas ces derniers signes...

cependant tu donnes toi même la réponse à ta dernière question

par **barbu23** » 20 Aoû 2007, 00:25

Malheureusement, il ne s'agit pas d'une suite de fonctions mais d'une fonction à deux variables

et

:

avec :

Donc, on ne peut pas tester la convergence uniforme !!

par **sandrine_guillerme** » 20 Aoû 2007, 00:32

quinto a écrit:Il y'a plein d'exemples où on peut intervertir les deux mais où il n'y a pas convergence uniforme.

AH bon?

pourtant c'est pas ce que j'ai dans mon cours..

par **sandrine_guillerme** » 20 Aoû 2007, 00:33

fahr451 a écrit:je ne comprends pas ces derniers signes...

cependant tu donnes toi même la réponse à ta dernière question

héy fahr, ce fut un bail !!

ça va ?

par **fahr451** » 20 Aoû 2007, 07:53

hello sandrine

oui oui fort bien ma foi et toi ?

par **Isomorphisme** » 20 Aoû 2007, 09:22

Bonjour

Elle est bizarre cette notation. Une somme sur un ensemble infini non dénombrable se note

et non

? (je suis d'accord, ce n'est que conventionnel)

Je me demande si tu n'as pas voulu écrire :

où

est la masse de Dirac en

(que tu dois connaître car j'ai l'impression que tu as utilisé la mesure de Lebesgues).

par **quinto** » 20 Aoû 2007, 14:16

Bon, je serais curieux de voir comment tu définis la somme sur un ensemble non dénombrable...

AH bon?
pourtant c'est pas ce que j'ai dans mon cours..

J'en doute fort.
Peut être devrais tu relire ton cours ...

par **quinto** » 20 Aoû 2007, 14:18

barbu23 a écrit:Est ce qu'on a droit d'intervertir ou non dans cet exemple là ?
Merci d'avance !!

Deja il faudrait comprendre ce que tu essaies de faire.
Tu ne m'expliques toujours pas ce que c'est que cette somme. Tu fais une somme sur un ensemble indénombrable, je suis assez curieux de voir comment ca peut avoir un sens...

par **quinto** » 20 Aoû 2007, 14:22

sandrine_guillerme a écrit:AH bon?
pourtant c'est pas ce que j'ai dans mon cours..

C'est pourtant assez évident de voir que c'est faux:

Soit f_n définie sur R par

Ces fonctions sont toutes intégrables, on a clairement que f_n converge simplement vers 0 (donc la limite est intégrable) et on a clairement aussi que la limite de l'intégrale est nulle.
Pourtant on n'a pas convergence uniforme vers 0.

Integrale d'une fonction continue !

Integrale d'une fonction continue !

Qui est en ligne