Integrale
40 messages
- Page 2 sur 2 - 1, 2
Si tu veut mon opinion (certains vont hurler), la notion de "valeur principale" d'une intégrale divergente est une espèce de "pis aller" lorsque l'on veut absoluement attribuer une valeur à une intégrale qui n'en a pas.
Au sens "purement mathématique", il me semble que la "bonne" façon de voir les intégrales est de les voir au sens de lebesgue (c'est là qu'on as le plus de résultats positifs) et la vision "lebesgue" est à l'opposé de la notion de valeur principale.
Je pense donc que ce type de calcul ne doit se faire que lorsque l'on a parfaitement assimilé la notion d'intégrales "usuelles", et en particulier le sens du théorème de Fubini (qui devient faux pour les calculs de valeurs principales)
Est-ce que tout ce que je te raconte est bien clair ?
Au sens "purement mathématique", il me semble que la "bonne" façon de voir les intégrales est de les voir au sens de lebesgue (c'est là qu'on as le plus de résultats positifs) et la vision "lebesgue" est à l'opposé de la notion de valeur principale.
Je pense donc que ce type de calcul ne doit se faire que lorsque l'on a parfaitement assimilé la notion d'intégrales "usuelles", et en particulier le sens du théorème de Fubini (qui devient faux pour les calculs de valeurs principales)
Est-ce que tout ce que je te raconte est bien clair ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
JeanJ a écrit:f(a,b,R)=Intégrale(Sqrt(R²-r²)*4*(r/(r+c))*K(p)*dr) pour 0<r<R
Sans avoir totalement résolu ce problème d'intégration, j'ai obtenu les premirers termes du développement selon les puissances entières de (c/R) :
f(a,b,R) = ((pi*R)²/2)*(1-(c/R)²/2+O((c/R)^4))
JeanJ est absent en ce moment. Je réfléchis beaucoup mais je ne suis pas arrivé à comprendre cette paragraphe au-dessus.
Quelqu'un pourrait m'aider à expliquer. Je vous remercie beaucoup.
Salut MSROE,
Concernant ce qu'a écrit JeanJ, je comprend parfaitement les calculs qu'il fait, là seule chose qui ne me parrait pas totalement claire, c'est le fait que la dérivée en 'a' de son intégrale (qui est absolument convergente) donnera bien la valeur principale de ton intégrale divergente. (formellement, c'est juste mais...)
Pour ta deuxième question, pour approximer l'intégrale, il a simplement fait un développement limité de la fonction à intégrer, puis il a intégré ce D.L.
P.S. Par simple curiosité, j'aimerais bien savoir pourquoi la valeur principale de cette intégrale divergente t'interesse...
Concernant ce qu'a écrit JeanJ, je comprend parfaitement les calculs qu'il fait, là seule chose qui ne me parrait pas totalement claire, c'est le fait que la dérivée en 'a' de son intégrale (qui est absolument convergente) donnera bien la valeur principale de ton intégrale divergente. (formellement, c'est juste mais...)
Pour ta deuxième question, pour approximer l'intégrale, il a simplement fait un développement limité de la fonction à intégrer, puis il a intégré ce D.L.
P.S. Par simple curiosité, j'aimerais bien savoir pourquoi la valeur principale de cette intégrale divergente t'interesse...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
JeanJ a écrit:Sans avoir totalement résolu ce problème d'intégration, j'ai obtenu les premirers termes du développement selon les puissances entières de (c/R) :
f(a,b,R) = ((pi*R)²/2)*(1-(c/R)²/2+O((c/R)^4))
.
C'est un problème très intéressant. Avant j'ai rencontré aussi un problème presque la même ce problème. Je vais le présenter à la suite. Mais d'abord, quelqu'un peux m'aider à expliquer plus clairement que comment JeanJ peut trouver cette solution après intégrale du développement au limite?
J'ai essayé avec K(p)=(pi/2)*(1+p^2/4) = (pi/2)*(1+r*c/(r+c)^2)
le la fonction sous le signe de l'intégrale est
sqrt(R^2-r^2)*(4*r/(r+c))*(pi/2)*(1+r*c/(r+c)^2)
Et comment vous pouvez continuer pour trouver le résultat?
JeanJ cherche à calculer  =\bigint\bigint_{D_R}\frac{\sqrt{R^2-x^2-y^2}}{\sqrt{(x-a)^2+(y-b)^2}}\,dx\,dy\) (où
(où  est le disque centré en 0 de rayon R) dont il affirme que la dérivée en
est le disque centré en 0 de rayon R) dont il affirme que la dérivée en  est la valeur principale de ton intégrable [si on dérive "formellement", c'est à dire sans se préocuper des problèmes de convergence, c'est vrai, mais ce n'est pas suffisant pour prouver un tel résultat...]. Cette intégrale, contrairement à celle de départ, a le bon gout d'être absolument convergente.
est la valeur principale de ton intégrable [si on dérive "formellement", c'est à dire sans se préocuper des problèmes de convergence, c'est vrai, mais ce n'est pas suffisant pour prouver un tel résultat...]. Cette intégrale, contrairement à celle de départ, a le bon gout d'être absolument convergente.
En passant en polaire et en posant=(r\cos(\varphi),r\sin(\varphi))) , on a :
, on a :
 =\bigint_0^{2\pi}\bigint_0^R \frac{\sqrt{R^2-\rho^2}}{\sqrt{\rho^2-2r\cos(\theta-\varphi)\rho+r^2}}\,\rho d\rho\,d\theta<br />=\bigint_0^R\rho\sqrt{R^2-\rho^2}\bigint_0^{2\pi}\frac{d\alpha<br />}{\sqrt{\rho^2-2r\cos(\alpha)\rho+r^2}}d\rho)
\,d\rho) où
où 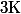 est l'intégrale éliptique complète de première espèce :
est l'intégrale éliptique complète de première espèce :
=\frac{\pi}{2} + \frac{\pi}{8}x^2 + \frac{9\pi}{128}x^4 +\frac{25\pi}{512}x^6 +\frac{1225\pi}{32768}x^8 +\...)
As tu demandé quel SENS peut on donner à la valeur principale d'une intégrale divergente dans le contexte qui t'interesse.
Ca me semble EXTREMEMENT suspect...........
En passant en polaire et en posant
As tu demandé quel SENS peut on donner à la valeur principale d'une intégrale divergente dans le contexte qui t'interesse.
Ca me semble EXTREMEMENT suspect...........
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
JeanJ a écrit:f(a,b,R) = ((pi*R)²/2)*(1-(c/R)²/2+O((c/R)^4))
Salut Ben314,
f(a,b,R)=Intégrale(sqrt(R^2-r^2)*(4*r/(c+r))*K(2*sqrt(r*c)/(r+c))) pour r=0..R
Est ce qu'on utilise le développement au limit:
K(x)=(pi/2)(1+x^2/4) --> K(2*sqrt(r*c)/(r+c)))=(pi/2)*(1+r*c/(r+c)^2)
Nous trouvons une approximation de f(a,b,R):
(pi/2)*Intégrale((sqrt(R^2-r^2)*(4*r/(c+r))*(1+r*c/(r+c)^2)) pou r=0..R
Et comment on peut continuer pour trouver le résultat de JeanJ au-dessus.
:briques:
Merci d'avance de votre enseignement.
Avant, j'ai du calculer une intégrale sur une disque (O,R) :
g(a,b,R) = intégrale(sqrt(R^2-r^2)*sqrt(r^2+c^2-2*r*c*cos(x-w)) pour r=0..R et x =0..2Pi. J'ai trouve également la forme
g(a,b,R)=intégrale(sqrt(R^2-r^2)*4*(r/(r+c))*E(p)) pour r=0..R et x =0..2P
Mais je sais pas pour continuer. Le résultat de JeanJ est un clé pour résoudre ce problème
Mais on n'a pas de chance parce que son absence. On va essayer d'attendre son retour pour expliquer plus clairement son idée
g(a,b,R) = intégrale(sqrt(R^2-r^2)*sqrt(r^2+c^2-2*r*c*cos(x-w)) pour r=0..R et x =0..2Pi. J'ai trouve également la forme
g(a,b,R)=intégrale(sqrt(R^2-r^2)*4*(r/(r+c))*E(p)) pour r=0..R et x =0..2P
Mais je sais pas pour continuer. Le résultat de JeanJ est un clé pour résoudre ce problème
Mais on n'a pas de chance parce que son absence. On va essayer d'attendre son retour pour expliquer plus clairement son idée
Ben314 a écrit:En passant en polaire et en posant, on a :
où
est l'intégrale éliptique complète de première espèce :
Bonjour,
Pourriez vous m'aider a expliquer comment vous pouvez trouver:
Intégrale(dx/sqrt(r^2+c^2-2*r*c*cos(x-w)) pour x=0..2Pi est égale K(2*sqrt(r*c)/(r+c)) ?
A ma part, je trouve que K(p)=Intégrale(dx/sqrt(1-p^2*(sinx)^2)
Mais ici, sqrt(r^2+c^2-2*r*c*cos(x-w))=sqrt(r^2+c^2-2*r*c*(1-2*(sin(x-w)/2)^2)=sqrt(r^2+c^2-2*r*c*(1-2*(sin(x-w)/2)^2)=
=sqrt((r-c)^2+4*r*c*(sin(x-w)/2)^2)
Bonjour,
La discussion qui a eu lieu au sujet de l'intégration en "valeur principale " de Cauchy est très significative des façon différentes d'appréhender certains problèmes selon qu'on est mathématicien ou physicien (du moins pour certains d'entre eux).
En effet, ces intégrales se rencontrent fréquemment en physique, ce qui heureusement ne gêne pas les personnes concernées et dont bon nombre intègrent et calculent la valeur principale sans la nommer, comme Monsieur Jourdain faisait de la prose sans le savoir.
Parfois même les mathématiciens le font aussi sans s'en rendre compte, lorsqu'ils utilisent une formule ou une fonction qui, sans en avoir l'air, a été établie grâce à une intégrale de ce genre. La fonction spéciale fréquemment utilisée Ei(x) en est un exemple typique et il y en a beaucoup d'autres.
Mais lorsque le cas est flagrant, comme par exemple l'intégrale de f(x)=1/x prise entre x=-2 et x=+1, le mathématicien dira que ce n'est pas intégrable et il aura raison : le domaine d'intégration inclut f(0) qui n'est pas fini.
Le physicien réagira tout différemment : >
C'est exactement ce que l'on fait en intégrant au sens de Cauchy (bien que plus raffiné en faisant tendre r vers 0). On ne va pas, à chaque fois, répéter la sempiternelle explication consistant à substituer localement à la fonction récalcitrante une quelconque fonction bornée et impaire.
Le puriste d'un coté et le praticien de l'autre ont tous deux raison et leurs discours sont respectivement exacts et cohérents, bien qu'apparemment contradictoires. Je ne vois pas ce qui nuirait à leur réconciliation et c'est déjà fait dans l'esprit de beaucoup, que ce soit empiriquement ou de façon plus théorique.
Ceci me rappelle un autre sujet de discordance, celui du calcul différentiel, qui a été l'objet d'une dissertation assez naïve : "Une querelle des Anciens et des Modernes".
http://www.scribd.com/people/documents/10794575-jjacquelin
Un papier du même acabit sur le sujet de l'intégration en valeur principale de Cauchy pourrait être tout aussi divertissant !
La discussion qui a eu lieu au sujet de l'intégration en "valeur principale " de Cauchy est très significative des façon différentes d'appréhender certains problèmes selon qu'on est mathématicien ou physicien (du moins pour certains d'entre eux).
En effet, ces intégrales se rencontrent fréquemment en physique, ce qui heureusement ne gêne pas les personnes concernées et dont bon nombre intègrent et calculent la valeur principale sans la nommer, comme Monsieur Jourdain faisait de la prose sans le savoir.
Parfois même les mathématiciens le font aussi sans s'en rendre compte, lorsqu'ils utilisent une formule ou une fonction qui, sans en avoir l'air, a été établie grâce à une intégrale de ce genre. La fonction spéciale fréquemment utilisée Ei(x) en est un exemple typique et il y en a beaucoup d'autres.
Mais lorsque le cas est flagrant, comme par exemple l'intégrale de f(x)=1/x prise entre x=-2 et x=+1, le mathématicien dira que ce n'est pas intégrable et il aura raison : le domaine d'intégration inclut f(0) qui n'est pas fini.
Le physicien réagira tout différemment : >
C'est exactement ce que l'on fait en intégrant au sens de Cauchy (bien que plus raffiné en faisant tendre r vers 0). On ne va pas, à chaque fois, répéter la sempiternelle explication consistant à substituer localement à la fonction récalcitrante une quelconque fonction bornée et impaire.
Le puriste d'un coté et le praticien de l'autre ont tous deux raison et leurs discours sont respectivement exacts et cohérents, bien qu'apparemment contradictoires. Je ne vois pas ce qui nuirait à leur réconciliation et c'est déjà fait dans l'esprit de beaucoup, que ce soit empiriquement ou de façon plus théorique.
Ceci me rappelle un autre sujet de discordance, celui du calcul différentiel, qui a été l'objet d'une dissertation assez naïve : "Une querelle des Anciens et des Modernes".
http://www.scribd.com/people/documents/10794575-jjacquelin
Un papier du même acabit sur le sujet de l'intégration en valeur principale de Cauchy pourrait être tout aussi divertissant !
Salut JeanJ,
Moi qui suis trés nettement du coté "mathématicien", je te fait absolument confiance en ce qui concerne le fait qu'en physique cette notion de "valeur principale" à un interêt.
Par contre peut tu m'expliquer pourquoi on considère que la fonction "dont on ne sait pas grand-chose" on la considère définie sur [-r,r] et pas plutôt (par exemple) sur [-r,2r] ? (dans ce cas, le résultat serait différent)
Evidement, sur ton exemple, le fait que x->1/x soit impaire peut conduire à dire (c'est ce que tu fait) qu'on admet qu'on ne connait pas g, mais qu'elle est elle aussi impaire et donc que son domaine de définition doit être symétrique par rapport à l'origine.
Mais, si à ta fonction f:x->1/x j'ajoute par exemple la fonction x->x² (qui est intégrable au voisinage de 0), le résultat n'est plus une fonction impaire.
Dans ce cas quel argument utiliser pour justifier que la partie "dont on ne tient pas compte" est symétrique par rapport à l'origine ?
P.S. Je le (re)dit : ne vois absolument aucune "critique" dans ces questions, je n'ai quasi jamais fait de physique ni de math. apliquées.
Ce sont réllement des questions de... curiosité...
Moi qui suis trés nettement du coté "mathématicien", je te fait absolument confiance en ce qui concerne le fait qu'en physique cette notion de "valeur principale" à un interêt.
Par contre peut tu m'expliquer pourquoi on considère que la fonction "dont on ne sait pas grand-chose" on la considère définie sur [-r,r] et pas plutôt (par exemple) sur [-r,2r] ? (dans ce cas, le résultat serait différent)
Evidement, sur ton exemple, le fait que x->1/x soit impaire peut conduire à dire (c'est ce que tu fait) qu'on admet qu'on ne connait pas g, mais qu'elle est elle aussi impaire et donc que son domaine de définition doit être symétrique par rapport à l'origine.
Mais, si à ta fonction f:x->1/x j'ajoute par exemple la fonction x->x² (qui est intégrable au voisinage de 0), le résultat n'est plus une fonction impaire.
Dans ce cas quel argument utiliser pour justifier que la partie "dont on ne tient pas compte" est symétrique par rapport à l'origine ?
P.S. Je le (re)dit : ne vois absolument aucune "critique" dans ces questions, je n'ai quasi jamais fait de physique ni de math. apliquées.
Ce sont réllement des questions de... curiosité...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re-bonjour,
en relisant les interventions récentes et dont je n'avais pas encore connaissance, je vois qu'il y a eu pas mal d'intérrogations au sujet de l'intervention dans laquelle j'annonçais le résultat -pi²a/2.
Je précise bien qu'il s'agissait d'un calcul fait hâtivement, incomplet et dont la démonstration n'est pas rigoureuse à ce stade. J'espérais que quelqu'un aurait trouvé, entre-temps, un méthode plus élégante et plus correcte. Il semble que ce ne soit pas encore le cas.
Je me sens donc moralement obligé de publier le calcul grossier que j'avais fait. Le puristes auront beau jeu pour dénoncer les manques de preuves et les points scabreux, un peu partout.
Tant pis, je me lance, en plaidant l'indulgence... (documents joints).
Désolé, mais je n'arrive pas à joindre les trois pages. Je les envoie à MSROE par message personnel, c'est lui le principal intéressé et c'est tout ce que je peux faire.
en relisant les interventions récentes et dont je n'avais pas encore connaissance, je vois qu'il y a eu pas mal d'intérrogations au sujet de l'intervention dans laquelle j'annonçais le résultat -pi²a/2.
Je précise bien qu'il s'agissait d'un calcul fait hâtivement, incomplet et dont la démonstration n'est pas rigoureuse à ce stade. J'espérais que quelqu'un aurait trouvé, entre-temps, un méthode plus élégante et plus correcte. Il semble que ce ne soit pas encore le cas.
Je me sens donc moralement obligé de publier le calcul grossier que j'avais fait. Le puristes auront beau jeu pour dénoncer les manques de preuves et les points scabreux, un peu partout.
Tant pis, je me lance, en plaidant l'indulgence... (documents joints).
Désolé, mais je n'arrive pas à joindre les trois pages. Je les envoie à MSROE par message personnel, c'est lui le principal intéressé et c'est tout ce que je peux faire.
La question était : pourquoi dans le cas de cette nouvelle fonction qui n'a pas de symétrie particulière par rapport à 0 continue-t-on à considérer que la partie "négligeable" est définie sur un intervalle centré en 0 ?JeanJ a écrit:...Je ne comprends pas bien la question...
Si tu veut, ce que je ne comprend pas du tout, c'est, dans le cas général (fonction non symétrique), qu'est ce qui justifie que l'on centre en 0 la partie que l'on "néglige" : pourquoi les intervalles [-r,r] jouent ils un rôle différent de ceux de la forme [-r,2r] ?
Ce qui me perturbe, c'est que l'on ne peut plus faire de changement de variable dans ce type de calcul, au niveau physique, cela me donne l'impression que l'on a un résultat qui dépend de l'unité choisie pour faire les mesures (changement de variable) et je trouve ça... surprenant !
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
La question était : pourquoi dans le cas de cette nouvelle fonction qui n'a pas de symétrie particulière par rapport à 0 continue-t-on à considérer que la partie "négligeable" est définie sur un intervalle centré en 0 ?
Tout ceci est dit de façon très résumée. Pour ne pas se compliquer la vie, on a pris l'exemple de la fonction 1/x
On aurait pu prendre la fonction 1/(x-2) par exemple et g(x) aurait été pris sur [2-r, 2+r].
La symétrie dont on parle est relative au point singulier, non à l'origine. Et ceci vaut respectivement pour chaque point singulier s'il y en a plusieurs.
La question n'est (évidement) pas sur le choix du point commun aux intervalles (qui est forcément la singularité) mais sur le fait du choix de centrer l'intervalle en ce point.
Si la singularité est en Pi, pourquoi [Pi-r,Pi+r] plutôt que [Pi-r,Pi+2r] (dans le cas où la fonction n'a pas de symétrie particulière autour du point Pi) ?
Si la singularité est en Pi, pourquoi [Pi-r,Pi+r] plutôt que [Pi-r,Pi+2r] (dans le cas où la fonction n'a pas de symétrie particulière autour du point Pi) ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Excuse-moi, Ben314, mais cette discussion me prend trop de temps sans utilité pour MSROE.
Dans mon post du 4/02 à 12h20, je me suis permis une longue digression (d'un niveau très élémentaire) en direction de la physique. Peut-être à tord car cela nous détourne du problème à résoudre. Un problème intéressant et d'un niveau pas du tout élémentaire.
Néanmoins, pour ceux qui entendent parler pour la première fois de "valeur principale de Cauchy" et qui souhaitent en avoir un minimum d'information :
http://fr.wikipedia.org/wiki/Valeur_principale_de_Cauchy
http://mathworld.wolfram.com/CauchyPrincipalValue.html
Dans mon post du 4/02 à 12h20, je me suis permis une longue digression (d'un niveau très élémentaire) en direction de la physique. Peut-être à tord car cela nous détourne du problème à résoudre. Un problème intéressant et d'un niveau pas du tout élémentaire.
Néanmoins, pour ceux qui entendent parler pour la première fois de "valeur principale de Cauchy" et qui souhaitent en avoir un minimum d'information :
http://fr.wikipedia.org/wiki/Valeur_principale_de_Cauchy
http://mathworld.wolfram.com/CauchyPrincipalValue.html
Bonjour,
Les résultats donnés précédemment étaient incomplets et approximatifs parce que les développements en série étaient limités au lieu d'être infinis. Ces derniers requièrent des connaissances approfondies de certaines fonctions spéciales : les intégrales elliptiques et la fonction hypergéométrique de Gauss, y compris dans leur domaine complexe.
Ceci se situant à un niveau probablement très supérieur à celui de MSROE, je me limite à donner le résultat final en tant qu'information : L'écriture des calculs intermédiaires serait trop volumineuse et difficilement acceptable sans un bon nombre de pré-requis ardus.
I = Somme double sur le disque de centre (0,0) et de rayon R de :
[Sqrt(R²-x²-y²)/Sqrt((x-a)²+(y-b)²)] dx dy
Avec c²=a²+b², on a déjà montré que :
I = 4 Somme pour r=0 à r=R de : (Sqrt(R²-r²))* (r/(r+c))*K[2Sqrt(c r)/(r+c)]*dr
Finalement, le développement en série des puissances entières de (c/R) est :
I = Sigma pour n=0 à n infini de Cn*(c²/R²)^n
avec Cn = -2*pi*R² [(2n)! / ((4^n)*(n!)²)]²(1/(2n-1))*F(A,B;C;X)
F(A,B;C;X) est la fonction hypergéométrique de Gauss, avec les paramètres suivants :
A = -1/2
B = (1-2n)/2
C = (3-2n)/2
X = 1.
Bien entendu, pour les valeurs négatives de C, il ne s'agit pas de la définition intégrale de cette fonction, mais de son prolongement. Les propriétés connues dans le cas particulier X=1 et pour les valeurs négatives de C=(3-2n)/2, c'est-à-dire pour n>1 , donnent
F(-1/2 , (1-2n)/2 ; (3-2n)/2 ;1) = 0
Donc Cn=0 pour tout n>1. Il ne reste que C0 et C1
F(-1/2 , 1/2 ; 3/2 ; 1) = pi/4 donc C0=-2pi*R²(1)²(-1)pi/4 = pi²*R²/2
F(-1/2 , -1/2 ; 1/2 ; 1) = pi/2 donc C1=-2pi*R²(2/4)²pi/2 = -pi²*R²/4
I = pi²*R²/2 (pi²*R²/4)(r²/R²)
I = (p²/2)*(R²-(r²/2)) = (pi²/2)*(R²-(a²+b²)/2)
La dérivation relativement à (a) conduit à :
Somme double sur le disque de centre (0,0) et de rayon R de :
[Sqrt(R²-x²-y²)*(x-a)/[(x-a)²+(y-b)²]^(3/2) dx dy = -pi²a/2
Ce qui est donc le résultat exact.
Etant bien conscient du fait que cette façon d'aboutir au résultat ne doit pas satisfaire MSROE parce qu'il n'en maîtrise pas toutes les étapes, il serait souhaitable que quelqu'un trouve une méthode plus élégante et surtout requièrant des connaissances plus élémentaires. Pour ma part, j'y ai déjà passé beaucoup trop de temps et j'en resterai donc là. Bon travail et avec mes souhaits de réussite à ceux qui voudront bien continuer sur ce sujet.
Les résultats donnés précédemment étaient incomplets et approximatifs parce que les développements en série étaient limités au lieu d'être infinis. Ces derniers requièrent des connaissances approfondies de certaines fonctions spéciales : les intégrales elliptiques et la fonction hypergéométrique de Gauss, y compris dans leur domaine complexe.
Ceci se situant à un niveau probablement très supérieur à celui de MSROE, je me limite à donner le résultat final en tant qu'information : L'écriture des calculs intermédiaires serait trop volumineuse et difficilement acceptable sans un bon nombre de pré-requis ardus.
I = Somme double sur le disque de centre (0,0) et de rayon R de :
[Sqrt(R²-x²-y²)/Sqrt((x-a)²+(y-b)²)] dx dy
Avec c²=a²+b², on a déjà montré que :
I = 4 Somme pour r=0 à r=R de : (Sqrt(R²-r²))* (r/(r+c))*K[2Sqrt(c r)/(r+c)]*dr
Finalement, le développement en série des puissances entières de (c/R) est :
I = Sigma pour n=0 à n infini de Cn*(c²/R²)^n
avec Cn = -2*pi*R² [(2n)! / ((4^n)*(n!)²)]²(1/(2n-1))*F(A,B;C;X)
F(A,B;C;X) est la fonction hypergéométrique de Gauss, avec les paramètres suivants :
A = -1/2
B = (1-2n)/2
C = (3-2n)/2
X = 1.
Bien entendu, pour les valeurs négatives de C, il ne s'agit pas de la définition intégrale de cette fonction, mais de son prolongement. Les propriétés connues dans le cas particulier X=1 et pour les valeurs négatives de C=(3-2n)/2, c'est-à-dire pour n>1 , donnent
F(-1/2 , (1-2n)/2 ; (3-2n)/2 ;1) = 0
Donc Cn=0 pour tout n>1. Il ne reste que C0 et C1
F(-1/2 , 1/2 ; 3/2 ; 1) = pi/4 donc C0=-2pi*R²(1)²(-1)pi/4 = pi²*R²/2
F(-1/2 , -1/2 ; 1/2 ; 1) = pi/2 donc C1=-2pi*R²(2/4)²pi/2 = -pi²*R²/4
I = pi²*R²/2 (pi²*R²/4)(r²/R²)
I = (p²/2)*(R²-(r²/2)) = (pi²/2)*(R²-(a²+b²)/2)
La dérivation relativement à (a) conduit à :
Somme double sur le disque de centre (0,0) et de rayon R de :
[Sqrt(R²-x²-y²)*(x-a)/[(x-a)²+(y-b)²]^(3/2) dx dy = -pi²a/2
Ce qui est donc le résultat exact.
Etant bien conscient du fait que cette façon d'aboutir au résultat ne doit pas satisfaire MSROE parce qu'il n'en maîtrise pas toutes les étapes, il serait souhaitable que quelqu'un trouve une méthode plus élégante et surtout requièrant des connaissances plus élémentaires. Pour ma part, j'y ai déjà passé beaucoup trop de temps et j'en resterai donc là. Bon travail et avec mes souhaits de réussite à ceux qui voudront bien continuer sur ce sujet.
JeanJ a écrit:I = 4 Somme pour r=0 à r=R de : (Sqrt(R²-r²))* (r/(r+c))*K[2Sqrt(c r)/(r+c)]*dr
Finalement, le développement en série des puissances entières de (c/R) est :
I = Sigma pour n=0 à n infini de Cn*(c²/R²)^n
avec Cn = -2*pi*R² [(2n)! / ((4^n)*(n!)²)]²(1/(2n-1))*F(A,B;C;X)
F(A,B;C;X) est la fonction hypergéométrique de Gauss
Bonjour
Tout est claire sauf la partie que j'ai cité ci-dessus. J'ai impression que c'est un point difficile et c'est pourquoi JeanJ n'ai pas présenté des détails.
Pourrais-tu ajouter quelques lignes pour expliquer la principe du developpement que vous avez trouver dessus pour satisfaire pas seulement MSROE mais également quelques autres intéressé à ce sujet.
Merci d'avance.
Bonjour "Numerical",
Je regrette, mais cela ne me semble pas possible matériellement sur ce forum.
Le principe de la méthode utilisée a été indiqué dans mes posts précédents (sommairement, je le reconnais). Mais pour aller plus loin, il faut "mettre la main dans le cambouis" et aller chercher des relations qui ne sont pas simples. En tout cas, ce serait trop difficile à expliquer sur le forum sans le support des équations écrites noir sur blanc !
J'ai recopié l'essentiel dans un document (5 pages), que je viens de compléter et de beaucoup simplifier par la même occasion. Il ne m'est pas possible de le mettre en document joint sur le forum.
Bien évidemment, si on me contacte par message privé (comme MSROE l'a fait) je l'adresserai en retour d'e-mail à qui souhaite l'obtenir.
Pourrais-tu ajouter quelques lignes pour expliquer la principe du developpement que vous avez trouver dessus pour satisfaire pas seulement MSROE mais également quelques autres intéressé à ce sujet.
Je regrette, mais cela ne me semble pas possible matériellement sur ce forum.
Le principe de la méthode utilisée a été indiqué dans mes posts précédents (sommairement, je le reconnais). Mais pour aller plus loin, il faut "mettre la main dans le cambouis" et aller chercher des relations qui ne sont pas simples. En tout cas, ce serait trop difficile à expliquer sur le forum sans le support des équations écrites noir sur blanc !
J'ai recopié l'essentiel dans un document (5 pages), que je viens de compléter et de beaucoup simplifier par la même occasion. Il ne m'est pas possible de le mettre en document joint sur le forum.
Bien évidemment, si on me contacte par message privé (comme MSROE l'a fait) je l'adresserai en retour d'e-mail à qui souhaite l'obtenir.
40 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
