Intégrale

[richmonder]

Bonjour!

Est-ce que vous pourriez me dire comment trouver l'intégrale de ln(x-1) svp ..

Merci d'avance

[le_fabien]

Bonjour,
en faisant une integration par partie.

[Daft Punk]

en dérivant x*ln(x-1), on trouve ln(x-1)+x/(x-1)

il faut donc "compenser" le x/(x-1)
pour cela, il me semble qu'il faut utiliser des artan ...

[sarr]

Essaye de passer par f '(x)g'o[f(x)] qui a pour primitive go[f(x)].
en posant f(x)=x+1 implik f '(x)=1
et g'(x)=ln(x). si tu conné pa la primitive de lnx:c'est xlnx-1
donc g(x)=xlnx-1
Applique go[f(x)] en raplacant les x par f(x) et tu trouve direct le resultat. et rederive pour verifier si t a bon ou pas.
Bonne chance

[Narhm]

Bonjour, une solution simple quand on ne connait pas de primitive de ln(x) est d'utiliser les intégrations par partie :
Ou g est une primitive de la fonction .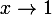
Il y en a une infinité, alors il faut bien choisir. En principe on se lance pour g(x)=x. Mais voyant la suite du problème pourquoi ne pas prendre g(x)=x-1 ?
Nous tombons sur quelque chose de simple :


On suppose la fonction ln(x-1) définie sur [a,b] bien sur.