Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
zoé
- Membre Naturel
- Messages: 21
- Enregistré le: 09 Déc 2007, 14:52
-
 par zoé » 01 Mai 2008, 20:03
par zoé » 01 Mai 2008, 20:03
\!\(
\*SubsuperscriptBox[\(\[Integral]\), \(-1\), \(1\)]\((\((x^2)\)
ArcSin[x])\)/\((\((1 + x^2)\)^\((1/2)\))\) \[DifferentialD]x\)
bonjour je n'arrive pas a calculer l'intégrale de -1 a 1 de (x^2arcsin[x])/(Sqrt(1+x^2))
Avec l'intégration par partie je tourne en rond...si quelqu'un pouvait maider??
Merci
pour info Mathematica me donne 0...si seulement il pouvait m'expliquer :we: ??
-
JQ_
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Mai 2008, 21:09
-
 par JQ_ » 01 Mai 2008, 21:16
par JQ_ » 01 Mai 2008, 21:16
Bonjour,
la complexité apparente de l'intégrale est là pour tromper l'ennemi ! Le résultat tient à deux choses : 1. on intègre sur [-1,1] et 2. ArcSin est une fonction impaire (les autres termes de l'intégrant étant x^2 tous pairs). Donc l'intégrale est nulle.
JQ_
-
mathelot
 par mathelot » 01 Mai 2008, 21:33
par mathelot » 01 Mai 2008, 21:33
c'est ce qui s'appelle "se faire avoir" :zen:
-
zoé
- Membre Naturel
- Messages: 21
- Enregistré le: 09 Déc 2007, 14:52
-
 par zoé » 01 Mai 2008, 21:45
par zoé » 01 Mai 2008, 21:45
c'est une explication mais je vois bien mon prof me rigoler au nez si je lui dit ca!
:ptdr:
une ptite idée pour le rédiger???
Danke
-
JQ_
- Membre Naturel
- Messages: 10
- Enregistré le: 01 Mai 2008, 21:09
-
 par JQ_ » 01 Mai 2008, 22:16
par JQ_ » 01 Mai 2008, 22:16

(relation de Chasles)
Dans la première intégrale on fait le changement de variable

alors

le carré étant pair et
 = -\arcsin(x) $)
l'arcsinus impair donc pour l'intégrant :

sous le changement de variable on a
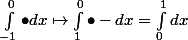
Tous comptes faits,
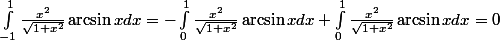
JQ_
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 66 invités
