Intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 16 Mai 2007, 17:17
par nnosch » 16 Mai 2007, 17:17
J'ai besoin de calculer l'intégrale suivante. Mais voila, comment faire?
^{5/6} \,dx.)
Merci!!!
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 16 Mai 2007, 18:56
par Pythales » 16 Mai 2007, 18:56
Je sais faire avec a=0, b=1 et c=1...
-
mehdi-128
- Membre Complexe
- Messages: 2838
- Enregistré le: 10 Déc 2006, 13:57
-
 par mehdi-128 » 16 Mai 2007, 18:58
par mehdi-128 » 16 Mai 2007, 18:58
Tu peux peut etre utiliser le binome de Newton et sortir la somme de l'intégrale.
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 08:56
par nnosch » 21 Mai 2007, 08:56
Merci pour votre aide, mais le cas a=0, b=c=1, n'est le cas qui m'intéresse...
Et le binôme de Newton de fonctionne qu'avec n entier naturel... et c'est non plus le cas qui m'intéresse...
Si vous avez d'autres idées je suis toujours préneurs.
Merci
-
abcd22
- Membre Complexe
- Messages: 2426
- Enregistré le: 13 Jan 2006, 14:36
-
 par abcd22 » 21 Mai 2007, 11:04
par abcd22 » 21 Mai 2007, 11:04
Bonjour,
Si on commence par ecrire
\)^{5/6} = \( - (x^2 -cx)\)^{5/6} = \( \frac{c^2}{4} - (x-\frac{c}{2})^2 \)^{5/6} = \(\frac{c^2}{4}\)^{5/6} \( 1 - \frac{4}{c^2}(x-\frac{c}{2})^2 \)^{5/6})
, puis poser
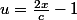
, on obtient
^{5/6})
(ou C est une constante).
Ensuite si on pose
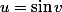
(ou

) on se retrouve avec une puissance de cosinus (ou sinus) a integrer, peut-etre qu'en posant
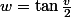
ou

ou

(ou autre puissance de cos ou sin) on trouve une integrale calculable, je n'ai pas de papier pour ecrire les calculs la. Il y a peut-etre plus simple mais je ne vois pas.
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 14:31
par nnosch » 21 Mai 2007, 14:31
Merci!
Il me reste plus qu'à calculer
^{11/6}\,dx)
.
Alors si quelqu'un a une idée...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 21 Mai 2007, 14:34
par fahr451 » 21 Mai 2007, 14:34
bonjour
je crois bien qu'il est inutile de chercher
d'où vient la prmière intégrale ?
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 15:04
par nnosch » 21 Mai 2007, 15:04
Bonjour,
J'essaye de minimiser une fonction dans laquelle l'équation 1 apparait. Du coup, j'aimerais bien calculer explicitement cette intégrale.
Je ne comprend pas pourquoi tu dis que c'est pas la peine de chercher?
As tu une autre piste pour le calcul de l'intégrale 1 (ou 2) qui peut aboutir?
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 15:19
par nnosch » 21 Mai 2007, 15:19
malheureusement non.
En vrai il faut que je trouve b (en fonction de c) qui minimise la fonction:
^{5/6}\,dx + \int_b^cx^{5/6}(c-x)^{5/6}\,dx)
D'ou l'idée de calculer explicitement l'intégrale en le tour est joué.
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Mai 2007, 16:30
par Pythales » 21 Mai 2007, 16:30
Effectivement, ton intégrale vaut
^{\frac{5}{6}}dx=c^{\frac{5}{6}}\int_0^cx^{\frac{5}{6}}(1-\frac{x}{c})^{\frac{5}{6}}dx)
en posant
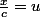
elle devient
^{\frac{5}{6}}du)
Je te renouvelle ma proposition ...
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Mai 2007, 16:31
par Pythales » 21 Mai 2007, 16:31
... du message #2
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 17:30
par nnosch » 21 Mai 2007, 17:30
Oui je suis d'accord avec vous... Mais une petite erreur c'est glissé dans mon expression de toute à l'heure (dsl). En fait la vrai c'est:
^{5/6}\,dx + \int_b^c(x-b)^{5/6}(c-(x-b))^{5/6}\,dx)
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 21 Mai 2007, 17:58
par nnosch » 21 Mai 2007, 17:58
Oui c'est vrai. Du coup il ne me reste plus qu'à calculer deux intégrales du type:
^{5/6}\,dx)
Ce qui n'est pas forcement aisé pour moi...
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 21 Mai 2007, 17:59
par fahr451 » 21 Mai 2007, 17:59
nnosch a écrit:Oui c'est vrai. Du coup il ne me reste plus qu'à calculer deux intégrales du type:
^{5/6}\,dx)
Ce qui n'est pas forcement aisé pour moi...
j 'en suis incapable
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 21 Mai 2007, 18:02
par B_J » 21 Mai 2007, 18:02
-
Pythales
- Habitué(e)
- Messages: 1162
- Enregistré le: 05 Déc 2005, 14:54
-
 par Pythales » 21 Mai 2007, 21:33
par Pythales » 21 Mai 2007, 21:33
Si
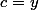
...
-
nnosch
- Messages: 9
- Enregistré le: 16 Mai 2007, 16:54
-
 par nnosch » 22 Mai 2007, 08:33
par nnosch » 22 Mai 2007, 08:33
Pythales a écrit:Si
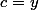
...
oui si c=y, alors c'est égal à
c^{8/3})
.
Mais c'est pas le cas, malheureusement!
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Mai 2007, 10:16
par B_J » 22 Mai 2007, 10:16
le lien ci-dessus te permet de calculer les primitives de ta fonction
-
fahr451
- Membre Transcendant
- Messages: 5142
- Enregistré le: 05 Déc 2006, 23:50
-
 par fahr451 » 22 Mai 2007, 10:18
par fahr451 » 22 Mai 2007, 10:18
B_J a écrit:le lien ci-dessus te permet de calculer les primitives de ta fonction
bonjour
tu as testé la fonction en question sur ton lien ?
-
B_J
- Membre Rationnel
- Messages: 621
- Enregistré le: 28 Aoû 2006, 02:21
-
 par B_J » 22 Mai 2007, 10:25
par B_J » 22 Mai 2007, 10:25
Salut Fahr
oui je l'ai testée
ca donne une primitive compliquée avec une fonction hypergeometrique
et c'est pour dire que les primitives de notre fonction ne s'exprime pas a l'aide des fonctions elementaires en nombre fini que j'ai proposé le lien :we:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
\)^{5/6} = \( - (x^2 -cx)\)^{5/6} = \( \frac{c^2}{4} - (x-\frac{c}{2})^2 \)^{5/6} = \(\frac{c^2}{4}\)^{5/6} \( 1 - \frac{4}{c^2}(x-\frac{c}{2})^2 \)^{5/6}) , puis poser
, puis poser 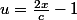 , on obtient
, on obtient ^{5/6}) (ou C est une constante).
(ou C est une constante). 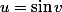 (ou
(ou  ) on se retrouve avec une puissance de cosinus (ou sinus) a integrer, peut-etre qu'en posant
) on se retrouve avec une puissance de cosinus (ou sinus) a integrer, peut-etre qu'en posant 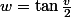 ou
ou  ou
ou  (ou autre puissance de cos ou sin) on trouve une integrale calculable, je n'ai pas de papier pour ecrire les calculs la. Il y a peut-etre plus simple mais je ne vois pas.
(ou autre puissance de cos ou sin) on trouve une integrale calculable, je n'ai pas de papier pour ecrire les calculs la. Il y a peut-etre plus simple mais je ne vois pas.