Intégrale

[Aispor]

Bonjours.
Pouvez-vous m'aider à montrer que la première intégrale converge, et à calculer la seconde ?
Merci !

[aviateur]

Bonjour
Pour la première intégrale la symétrie par rapport à 1/2 fait que le problème est le même en t=0 et t=1.
Donc il suffit de regarder ce qu'il se passe en t=0. Mais en t=0 la fonction est équivalente à
et tu dois pouvoir répondre si tu est capable de dire si est convergente.
Remarque cette intégrale mérite d'être calculée, c'est faisable.

Pour le calcul de la seconde intégrale, il y a plusieurs façon de faire mais le + direct est de passer par les complexes en remplaçant sin(t) par exp(i*t) et puis faire une ipp pour tuer le terme polynomial t.
La réponse est 1/2.

[Aispor]

Merci aviateur. Je n'avais pas du tout penser à la symétrie ^^

Oups désolé mais enfaite je me suis trompé c'est pas la deuxième qu'il fallait calculer x)
C'est celle-ci :



J'ai réussis à montrer qu'elle convergeait.
J'ai essayer une IPP et un changement de variable mais sans succès

[Elias]

Salut, une IPP marche :



avec et

donc et

Le produit s'intègre bien :




Remarque : attention, il est très important de bien manipuler les bornes avant de faire ton IPP (en calculant ton intégrale d'abord sur un segment puis en passant à la limite) car il y a des trucs qui vont se regrouper...

[Aispor]

Merci bcp!!
Du coup j'ai trouvé une intégrale nulle
En effet je voulais directement passé à la limite est j'ai loupé les simplifications avec les bornes

[Ben314]

Salut,
Sinon, si ça t'amuse, l'intégrale , non seulement elle est convergente, mais en fait elle se calcule (relativement) facilement...

[aviateur]

Oui l'intégrale est bien nulle. On peut le voir sans faire une IPP.
En effet
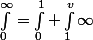
Puis dans l'intégrale faire le changement de variable t=1/u

[Aispor]

Hello Ben.
Peux tu me donner un petit indice ? ^^

Merci Aviateur ! Ça marche du tonnerre :p
Mais comment tu vois ça ? Une méthode en particulier ?

[mathelot]

bsr,



on fait le changement de variable

[mathelot]

Salut,
Sinon, si ça t'amuse, l'intégrale , non seulement elle est convergente, mais en fait elle se calcule (relativement) facilement...

On trouve

[Aispor]

Bsr matelot !
Bien beau la chgt de variable.
Peux tu me dire comment tu as fais pour trouver la deuxième intégrale? Je pense qu'il y a un petit arcsin mais je n'arrive pas à le faire apparaître.

[mathelot]

Il y a une merveilleuse suite numérique dite suite logistique qui vérifie


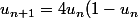on l'étudie en posant

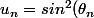dc pour la première intégrale
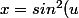poser avec

[aviateur]

Hello Ben.
Merci Aviateur ! Ça marche du tonnerre :p
Mais comment tu vois ça ? Une méthode en particulier ?

Non il n'y a pas de méthode ici, sinon que de voir que u=1/t transforme ton intégrale en une intégrale du même genre.
c'est à dire une intégrale avec ln(u) et une fraction rationnelle en u. Cela vaut le coup de regarder.
Disons que quand tu me dis que l'intégrale vaut 0 ça m'incite à regarder!

Pour le calcul de c'est très simple.
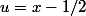
Tu fais le chgement de variable pour profiter de la symétrie.
Il vient
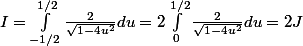
Et puis pour calculer J et effectivement voir du arcsinus tu peux faire v=2u, il va apparaitre à un facteur près
la dérivée de arcsinus(v). Le calcul est aisé.
On doit trouver

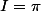
[aviateur]

Rebonjour
Je n'avais pas vu la proposition de @mathelot mais ça marche aussi bien sûr.

[Pisigma]

Bonjour,

autre piste

[aviateur]

OK @Psigma

[Aispor]

Merci pour toutes ces astuces ! =)