Intégrale

par **Calvinator2000** » 19 Mai 2015, 20:18

Bonsoir,

Soit

continue par morceaux, croissante.
On supose qu'il existe

Montrer que

En déduire que

diverge.

J'ai éssayé le changement de variable

mais je ne peux rien en conclure.
Comment faire?

par **Matt_01** » 19 Mai 2015, 21:35

Il manque pas certaines hypothèses ?
Par exemple avec f(x)=x+rac(x) (définie sur [1;+inf[) on a f(1) = 2 et donc x0=1 et lambda=1 convient. En somme f vérifie les conditions. Seulement l'intégrale définie converge (c'est équivalent à du x^(-3/2)).

par **Calvinator2000** » 19 Mai 2015, 22:27

J'ai relu l'énoncé et il ne donne pas d'autres hypothèses...
Mis à part que

sans quoi

n'est pas défini.
Ta fonction contredit l'énoncé, j'en déduis que l'énoncé est faux...

Cependant, la 2ème question de l'énoncé est :

Montrer que si

converge, alors

Ce qui est assez étrange compte tenu de la première question...

Merci.

par **Ben314** » 20 Mai 2015, 20:52

Salut,
Un truc que je verrais bien comme erreur d'énoncé, c'est :

Calvinator2000 a écrit:Soit continue par morceaux, croissante.
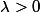
On suppose qu'il existe et tels que ...

Mais j'ai ça rend le truc passablement trivial...

EDIT :
Par contre le résultat de la question 2) est correct, mais pour la 1), je vois vraiment pas comment "tripoter" l'énoncé pour le rendre cohérent...
En particulier la minoration l'intégrale de xo à (1+lambda)xo par l'intégrale de 1 à 1+lambda, ben :
- Je voit pas d'où elle pourrait sortir (i.e. quelles hypothèse ajouter)
- Je vois pas à quoi ça peut servir vu que l'intégrale de 1 à 1+lambda peut parfaitement être nulle et que dans ce cas, l'inégalité va pas apporter grand chose...

par **Calvinator2000** » 20 Mai 2015, 22:17

Merci Matt et Ben pour vos réponses.

Tant pis pour la première question dont l'énoncé semble faux.

par **Ben314** » 20 Mai 2015, 23:02

Ce qui est d'autant plus bizare, c'est que, pour prouver le résultat de la question 2), il semble effectivement logique de montrer que,
Si

alors

Mais je vois toujours pas comment "bricoler" la question 1) avec son intégrale de 1 à lambda comme minorant...
(et ça m'énerve... :hum:)

par **mathelot** » 21 Mai 2015, 07:53

par curiosité, d'où provient cet énoncé faux ?
d'un établissement scolaire, d'une traduction, d'une création personnelle, d'une blague?

par **Matt_01** » 21 Mai 2015, 10:47

L'intégrale peut être minorée par

Si on remplace l'énoncé par

,

alors on peut déduire la divergence de l'intégrale (dans [1, +inf[ on peut trouver une infinité d'intervalles disjoints de type [x0,(1+lambda)x0] et donc leurs intégrales ne peuvent être minorées par la même constante non nulle si on veut la convergence de l'intégrale). Et alors l'énoncé tendrait à vouloir démontrer

pour avoir la convergence.

par **Calvinator2000** » 21 Mai 2015, 17:59

mathelot a écrit:par curiosité, d'où provient cet énoncé faux ?
d'un établissement scolaire, d'une traduction, d'une création personnelle, d'une blague?

Il vient d'un TD de mathématiques de mon prof de sup. Mais nous ne l'avions pas abordé.

Intégrale

Intégrale

Qui est en ligne