Intégrale
14 messages
- Page 1 sur 1
Intégrale
Bonjour,
Je cherche à calculer l'intégrale de e^(-r*sin²;))drd;)
Javoue que je ne trouve pas la solution.
Y a t-il une solution analytique ?
si oui, je pense qu'il y a un changement de variable.
Quelqu'un aurait-il une idée ?
Merci d'avance
Je cherche à calculer l'intégrale de e^(-r*sin²;))drd;)
Javoue que je ne trouve pas la solution.
Y a t-il une solution analytique ?
si oui, je pense qu'il y a un changement de variable.
Quelqu'un aurait-il une idée ?
Merci d'avance
Je prends la main après quelque raccourci : l'intégrale ) de
de =e^{-r*sin^2{\theta}) est à calculer...
est à calculer...
Soit R une surface du plan délimitée par la courbe continue) et les demi-droites :
et les demi-droites :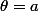 et
et 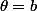 , où
, où
 (a et b étant des réels) alors la superficie S de cette surface vaut
(a et b étant des réels) alors la superficie S de cette surface vaut 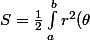 \;\mathrm{d}\theta) .
.
Un élément d'aire infinitésimale est vu comme :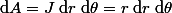 ou
ou 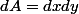
avec le Jacobien de la matrice de conversion des coordonnées qui est l'opérateur ici:
le Jacobien de la matrice de conversion des coordonnées qui est l'opérateur ici:
}{\partial(r,\theta)}<br />=\begin{vmatrix}<br /> \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\<br /> \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta}<br />\end{vmatrix}<br />=\begin{vmatrix}<br /> \cos\theta & -r\sin\theta \\<br /> \sin\theta & r\cos\theta<br />\end{vmatrix}<br />=r\cos^2\theta + r\sin^2\theta = r) .
.
Maintenant une fonction donnée en coordonnées polaires peut être intégrée comme ceci :
 \;\mathrm{d}A = \int_a^b \int_0^{r(\theta)} f(r,\theta) \;r \mathrm{d}r \;\mathrm{d}\theta) .
.
R est la même aire que celle comprise entre la courbe :) et les demi-droites
et les demi-droites 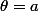 et
et 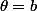 .
.
Sur} \subset \mathbb{R_{+}^{*}} \subset \mathbb{R}) et
et } \subset[0, \theta] \subset [0, 2\pi]) ,
,
Remarquons que :)*rdrd\theta) où :
où :  =e^{-r*sin^2{\theta}}) peut aider à calculer
peut aider à calculer )
en ayant au préalable le résultat intermédiaire suivant :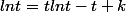 où
où  et
et 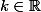
et après des changements de variable en et en
et en  puis en intégrant par parties et en résolvant une équation différentielle ou un autre type d'équation en
puis en intégrant par parties et en résolvant une équation différentielle ou un autre type d'équation en ) : l'hypothèse était au moins à prévoir ici...
: l'hypothèse était au moins à prévoir ici...
Soit R une surface du plan délimitée par la courbe continue
Un élément d'aire infinitésimale est vu comme :
avec
Maintenant une fonction donnée en coordonnées polaires peut être intégrée comme ceci :
R est la même aire que celle comprise entre la courbe :
Sur
Remarquons que :
en ayant au préalable le résultat intermédiaire suivant :
et après des changements de variable en
Salut Babe,
dans cette discussion, tous les malentendus viennent du fait que tu as posé ton problème de façon ambiguë.
En effet, il ne s'agit pas d'une intégration à une seule variable, mais d'une intégration à deux variables. Comme cela a été répété par des intervenants précédents, il faut que tu définisses précisément le domaine d'intégration, c'est à dire les bornes des deux intégrales.
Si ce domaine n'est pas défini, la résolution analytique nécessite de préciser si les deux variables (r et thêta) sont indépendantes ou sont liées par une relation qu'il faudrait fournir.
En l'absence de ces données dans l'énoncé du problème, tu ne recevras aucune solution cohérente.
dans cette discussion, tous les malentendus viennent du fait que tu as posé ton problème de façon ambiguë.
En effet, il ne s'agit pas d'une intégration à une seule variable, mais d'une intégration à deux variables. Comme cela a été répété par des intervenants précédents, il faut que tu définisses précisément le domaine d'intégration, c'est à dire les bornes des deux intégrales.
Si ce domaine n'est pas défini, la résolution analytique nécessite de préciser si les deux variables (r et thêta) sont indépendantes ou sont liées par une relation qu'il faudrait fournir.
En l'absence de ces données dans l'énoncé du problème, tu ne recevras aucune solution cohérente.
LaCoc6nl a écrit:JeanJ, ma solution en accord avec les règles de l'intégration double est valide en tout cas de figures, même aux limites...
Tu commences par : >
C'est justement ce qu'on demande à Babe de confirmer et de préciser.
Dans l'énoncé de son problème, il n'est pas dit qu'il y a une courbe limitant le domaine, si elle est continue, si son équation est connue ou non, si elle est définie par une fonction de la forme r(theta) ou sous une forme totalement différente : paramétrique, ou implicite, ou autre, ...
Mieux vaut attendre que le problème soit bien posé avant de faire des suppositions et des développements qui peuvent être infondés.
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
