Intégrale, f(sin(x), cos(x))
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Math3matiqu3
- Membre Relatif
- Messages: 124
- Enregistré le: 19 Avr 2013, 19:14
-
par Math3matiqu3 » 08 Mai 2020, 03:07
Bonsoir,
Calculer l'intégrale :
}{1 + cos(x)}\, \mathrm{d}x)
Par changement de variable
)
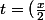, on aura :
et
)
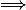
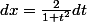
 = \frac{2t}{1+t^2})
et
 = \frac{1-t^2}{1+t^2})
En remplaçant dans notre intégrale et après simplification, j'obtiens :
 \mathrm{d}t)
Puis, j'ai essayé une intégration par partie avec
 = \frac{2t}{1+t^2} et v(x) = arctg(t))
j'ai obtenu :
 ln(1+t^2)\overset{+ \infty}{\underset{0}{]}})
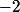
}{1+t^2} \mathrm{d}t)
Je ne sais pas comment avancer plus que ça..
Quelqu'un a une idée ?
Merci !
-
GaBuZoMeu
- Habitué(e)
- Messages: 6132
- Enregistré le: 05 Mai 2019, 09:07
-
par GaBuZoMeu » 08 Mai 2020, 06:54
Est-ce que l'intégrale (impropre) converge en
?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 48 invités
