Bonjour je dois faire l'intégrale de 0 à 2pi de sin(x)^2.cos(x)^4 , mais je ne vois pas comment le faire.
Merci de vos réponse.
Intégrale Sin Cos
6 messages
- Page 1 sur 1
Salut
Tout à fait Luc!
Et partant de cette idée le seul terme qui reste à intégrer est la constante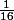 ce qui donne
ce qui donne 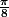 comme résultat de l'intégrale
comme résultat de l'intégrale
On voit que cela se fait sans le moindre calcul de primitive.
Luc a écrit:Et surtout, ne calcule pas les intégrales de 0 à 2pi de cos(kx) avec k entier! Elles sont toutes nulles, car on intègre sur un nombre entier de périodes.
Tout à fait Luc!
Et partant de cette idée le seul terme qui reste à intégrer est la constante
On voit que cela se fait sans le moindre calcul de primitive.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 25 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
