Bonjour, bonsoir à tous
Jai un problème avec un exercice et je narrive pas à trouver la solution, jespère que vous pourrez maider
Alors voilà lexo :
On pour tout n ;) N,
I_n=;)(0 à ( pi/2)););) cos;)(t) ;) dt
a) Calculer I_(0) et I_(1).
b) Démontrer que pour tout n ;) N, on a : 0< I_(n+1)< I_n.
c) Etablir pour tout n>=2 la relation : n*I_n=(n-1)*I_(n-2).
d) En déduire que n*I_n* I_(n-1)=pi/2 pour tout n >=1, puis calculer I_n en fonction de n (on traitera dabord le cas n pair en utilisant la question c) puis le cas n impair à laide de légalité précédente ).
e) Déduire des questions précédentes que
I_n/I_(n-1) -->1 lorsque n-->+inf puis que ;)n*I_n --> ;)pi/;)2 lorsque n-->+inf
Voilà en ce qui concerne lénoncé. Jai réussi à faire les questions a) b) c)
Mais je bloque à la d) et e) ^^
merci par avance.
Integrale et primitive
4 messages
- Page 1 sur 1
Salut !
En prenant l'égalité obtenue dans c), et multipliant membre à membre par ce qui manque pour avoir le même membre de gauche dans l'égalité de d), on a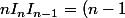 I_{n-1} I_{n-2}) .
.
Un récurrence immédiate donne alors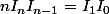 .
.
Ensuite, si n est pair alors il s'écrit sous la forme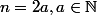 .
.
On a alors, d'après c),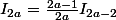 .
.
Fait encore une récurrence immédiate (même raisonnement pour ).
).
amine3030 a écrit:c) Etablir pour toutla relation :
.
d) En déduire quepour tout
, puis calculer
en fonction de
(on traitera dabord le cas
pair en utilisant la question c) puis le cas
impair à laide de légalité précédente ).
En prenant l'égalité obtenue dans c), et multipliant membre à membre par ce qui manque pour avoir le même membre de gauche dans l'égalité de d), on a
Un récurrence immédiate donne alors
Ensuite, si n est pair alors il s'écrit sous la forme
On a alors, d'après c),
Fait encore une récurrence immédiate (même raisonnement pour
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
amine3030 a écrit:j'ai compris pour la première partie de la question mais j'ai pas bien saisi comment t'as fais pour le cas de n pair, ni impair d'ailleurs :p
il faut calculer I_2p ?
Oui, j'avais mis des
C'est un peu la même chose que pour la première partie de la question : il faut faire une récurrence immédiate.
On a
En posant n=2a, on a
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
