Intégrale pour physicien en détresse

[Babe]

Bonjour à tous

j'ai une intégrale a calculer mais elle veut pas se laisser attraper
si quelqu'un a un plus grand lasso que moi je suis preneur



merci d'avance

[ffpower]

En mettant e^x en facteur puis en developpant 1/(1-e^(-x)) en serie,j obtient que ca vaut zeta(4)*integrale de x^3e^(-x)=pi^4/15.Mais ce serait bien que qqun comfirme(ps:dsl,j avais la flemme de taper en latex..)

[alavacommejetepousse]

bonsoir

je trouve pareil.

[alben]

Bonjour,
Ton intégrale peut s'écrire

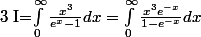
On peut faire ça avec les résidus ou par les séries :
la fonction est positive et majorée par , on peut donc écrire
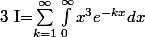
Les intégrales se calculent facilement avec quelques IPP et l'on tombe sur la somme de la série 1/(k^4), bien connue

[Babe]

oula c'est plus dur que prévu
donc je met en facteur

puis apres tu veux dire quoi par developpement ?

[Babe]

oups grillé par alben

ok merci à vous

oui le résultat est bien pi^4/15 (qui etait donné dans mon enoncé) mais je voulais savoir faire tout seul lol

[Babe]

y a t-il une quelconque approximation ou le résultat est exacte de chez exacte ?

[alavacommejetepousse]

résultat exact

[Babe]

pour calculer la somme des 1/k^4 ya t-il une methode simple comme pour la somme des 1/k^2 avec les serie de fourier ?
(pourquoi en parcours physique on fais pas les series grrr !)

[alavacommejetepousse]

oui avec les séries de fourier c 'est simple

[Babe]

ok je vous remercie bien