Intégrale par changement de variable
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
smike2809
- Messages: 9
- Enregistré le: 09 Avr 2014, 12:47
-
 par smike2809 » 13 Avr 2014, 18:23
par smike2809 » 13 Avr 2014, 18:23
Bonjour,
Toujours dans le chapitre intégrale par changement de variable je bloque sur deux exercices:


Merci
-
chbichib
- Membre Naturel
- Messages: 28
- Enregistré le: 06 Mar 2010, 16:39
-
 par chbichib » 13 Avr 2014, 18:33
par chbichib » 13 Avr 2014, 18:33
pour la première tu ajoute 2 et tu retranche 2 du numérateur
et la deuxième c une integ par partie ( 2 ou 3 fois)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 13 Avr 2014, 18:37
par zygomatique » 13 Avr 2014, 18:37
salut
je ne vois pas l'intérêt de faire un changement de variable pour la première ...
il suffit d'écrire :: 4x = 2(2x + 1) - 2
pour la deuxième peut-être .... et encore ....
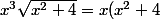^{3/2} - 4x \sqrt {x^2 + 4})
les deux termes sont deux la forme

avec n = fraction ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
deltab
- Membre Rationnel
- Messages: 806
- Enregistré le: 18 Juin 2013, 09:12
-
 par deltab » 13 Avr 2014, 21:06
par deltab » 13 Avr 2014, 21:06
Bonsoir.
smike2809 a écrit:Bonjour,
Toujours dans le chapitre intégrale par changement de variable je bloque sur deux exercices:


Merci
Dans ce genre d'exercices, on suppose qu'il existe un changement de variables pour lequel l'intégrale obtenue est simple à calculer mais ce n'est pas nécessairement la meilleure méthode.
On peut poser
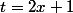
pour la première et
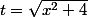
en remarquant
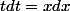
(On aboutit à l'intégration d'un polynôme en

)
-
smike2809
- Messages: 9
- Enregistré le: 09 Avr 2014, 12:47
-
 par smike2809 » 13 Avr 2014, 21:37
par smike2809 » 13 Avr 2014, 21:37
Alors pour le premier j'ai fais ceci:
Par contre ça ne correspond pas à la solution

Pour le 2e exercice, la donné indique de résoudre par un changement de variable. Est-ce quand même possible? si oui par quels moyens. (Les intégrations par parties est le prochain chapitre, nous ne l'avons pas encore étudié)
-
fibonacci
- Membre Relatif
- Messages: 492
- Enregistré le: 21 Mai 2006, 08:50
-
 par fibonacci » 14 Avr 2014, 03:28
par fibonacci » 14 Avr 2014, 03:28
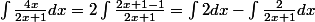
le changement de variable ne se fait que sur l'expression qui contient x
remarque
^' = \frac{{u^' }}{u})
^{\frac{3}{2}} \\ <br /> \int {(X^2 - 4)^{\frac{3}{2}} X\frac{X}{{\sqrt {X^2 - 4} }}} dX = \int {(X^2 - 4)X^2 } dX \\ <br /> \end{array})
-
Black Jack
 par Black Jack » 14 Avr 2014, 10:31
par Black Jack » 14 Avr 2014, 10:31
S x³(x²+1)^(1/2) dx
Poser x²+4 = t²
x dx = t dt
x² = (t²-4)
S x³(x²+1)^(1/2) dx = S (t²-4).t² dt = S (t^4 - 4t²) dt = t^5/5 - 4t³/3 = (1/5).(x²+4)^(5/2) - (4/3) * (x²+4)^(3/2) = (1/15).(x²+4)^(3/2)*(3x²+12-20) = (1/15).(x²+4)^(3/2)*(3x²-8)
F(x) = (1/15).(x²+4)^(3/2)*(3x²-8) est une primitive de f(x) = x³(x²+1)^(1/2) dx
:zen:
-
smike2809
- Messages: 9
- Enregistré le: 09 Avr 2014, 12:47
-
 par smike2809 » 14 Avr 2014, 14:48
par smike2809 » 14 Avr 2014, 14:48
merci pour votre aide je regarde tout ça.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 14 Avr 2014, 15:40
par zygomatique » 14 Avr 2014, 15:40
smike2809 a écrit:merci pour votre aide je regarde tout ça.
[|QUOTE]salut
je ne vois pas l'intérêt de faire un changement de variable pour la première ...
il suffit d'écrire :: 4x = 2(2x + 1) - 2
pour la deuxième peut-être .... et encore ....
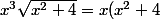^{3/2} - 4x \sqrt {x^2 + 4})
les deux termes sont deux la forme

avec n = fraction ....[/quote]
le changement de variable est écrit à la dernière ligne ... nul besoin de l'expliciter lorsqu'on a fait une première et une terminale ...
:lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités






