bonjours a tous,
je planche sur un problème sur les intégrales impropres.
"Pour quelles valeurs de alpha I=int(-inf à +inf) de (1/(1+x²)^alpha)dx converge?" .
J'ai réussi à montrer que pour alpha=1 I converge mais dans le cas alpha différent de un je n'arrive pas à trouver d'intégrale de 0 a x de 1/((1+x²)^alpha).
Je dois ensuite trouver une relation entre I(alpha) et I(alpha+1) c'est pourquoi je pense que je dois trouver l'intégrale de 0 a x de 1/((1+x²)^alpha) pour résoudre cette deuxième question avec une intégration par partie...
Si quelqu'un pouvait m'aider svp.
Intégrale impropre
4 messages
- Page 1 sur 1
Salut,
pour commencer on peut se restreindre a a cause de la symetrie.
a cause de la symetrie.
Apres, il me semble qu'on peut comparer ce qu'il y a sous l'intégrale avec un équivalent.
Du coup, on peut chercher un équivalent de^\alpha}) en l'infini et en 0
en l'infini et en 0
En l'infini, on peut ecrire la forme exponentielle :
)=exp( \alpha ln(x^2(1+\frac{1}{x^2})))=exp(2 \alpha ln(x)+o(x)))
avec
Du coup, on peut faire une analogie avec le critère de Riemann ou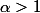 donne la CV de
donne la CV de 
Pour 0, il suffit de faire un DL de^\alpha)
Après, sous réserve qu'on peut utilise les équivalents :marteau:
pour commencer on peut se restreindre a
Apres, il me semble qu'on peut comparer ce qu'il y a sous l'intégrale avec un équivalent.
Du coup, on peut chercher un équivalent de
En l'infini, on peut ecrire la forme exponentielle :
avec
Du coup, on peut faire une analogie avec le critère de Riemann ou
Pour 0, il suffit de faire un DL de
Après, sous réserve qu'on peut utilise les équivalents :marteau:
la vie est une fête 
Bonjour may prepa,
tu as écrit :
<< Je dois ensuite trouver une relation entre I(alpha) et I(alpha+1) c'est pourquoi je pense que je dois trouver l'intégrale de 0 a x de 1/((1+x²)^alpha) >>
C'est une faute de raisonnement très répendue, beaucoup trop fréquente !!!
En effet, l'intégrale de 0 à +inf d'une fonction peut parfois être facile à calculer, alors qu'au contraire l'intégrale de 0 à x peut être très difficile, voire impossible sans des connaissances d'un niveau suppérieur.
C'est justement le cas de ce problème : Pour la fonction donnée, l'intégrale de 0 à x ne s'exprime pas avec les fonctions usuelles. Il faudrait connaitre certaines fonctions spéciales.
Il est clair qu'on ne demande pas de la calculer : On doit répondre aux questions posées sans calculer l'intégrale de 0 à x. Et on doit aboutir à la formule de l'intégrale de 0 à +inf sans avoir besoin de connaitre celle de 0 à x.
tu as écrit :
<< Je dois ensuite trouver une relation entre I(alpha) et I(alpha+1) c'est pourquoi je pense que je dois trouver l'intégrale de 0 a x de 1/((1+x²)^alpha) >>
C'est une faute de raisonnement très répendue, beaucoup trop fréquente !!!
En effet, l'intégrale de 0 à +inf d'une fonction peut parfois être facile à calculer, alors qu'au contraire l'intégrale de 0 à x peut être très difficile, voire impossible sans des connaissances d'un niveau suppérieur.
C'est justement le cas de ce problème : Pour la fonction donnée, l'intégrale de 0 à x ne s'exprime pas avec les fonctions usuelles. Il faudrait connaitre certaines fonctions spéciales.
Il est clair qu'on ne demande pas de la calculer : On doit répondre aux questions posées sans calculer l'intégrale de 0 à x. Et on doit aboutir à la formule de l'intégrale de 0 à +inf sans avoir besoin de connaitre celle de 0 à x.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
