Intégrale impropre

par **ayla8101** » 18 Oct 2006, 18:04

Je dois montrer que l'intégrale impropre qui va de 1 en +l'infini de la fonction f(x) = lnx/(1+x²) converge et déterminer sa valeur.
Pourriez vous m'ai dez svp?

par **isortoq** » 19 Oct 2006, 13:47

ayla8101 a écrit:Je dois montrer que l'intégrale impropre qui va de 1 en +l'infini de la fonction f(x) = lnx/(1+x²) converge et déterminer sa valeur.
Pourriez vous m'ai dez svp?

N'est-ce pas plutôt : f(x) = lnx/(1+x)² ??

par **ayla8101** » 19 Oct 2006, 18:26

non c'est bien la bonne forme. Apparemment je ne suis pa la seule à ne pas trouver..

par **yos** » 19 Oct 2006, 18:36

Et si c'était 0 la borne inférieure?? Dans ce cas l'intégrale vaudrait 0.
Remarque : la convergence est triviale car l'intégrande est un o(x^(-3/2))

par **ayla8101** » 19 Oct 2006, 18:54

non la borne inferieure est 1. Enfin ce n'est pas grave je demanderias à quelqu'un de ma classe comment m'y prendre!Merci

par **tize** » 19 Oct 2006, 21:54

N'oublie pas de nous donné la réponse si tu l'as stp...

par **tize** » 20 Oct 2006, 08:49

J'ai posté la question sur un autre forum (ici ) , pour l'instant pas de réponse mais quelqun a proposé un changement de variable (x=1/t) et on obtient le résultat suivant :

Ca m'a donné une idée : ne peut on pas developper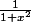

sous forme de série que l'on pourra ensuite sortir de l'intégrale de a à b puis faire tendre a vers 0 et b vers 1 (bord du domaine de convergence de la série)...
Je vais essayer

par **tize** » 20 Oct 2006, 10:25

J'ai essayé d'avancer le problème ici : http://www.mathematex.net/phpBB2/ici-vp11049.html#11049
il semblerait que cela donne :

mais j'ai des petits soucis (comme vous pourrez le lire) pour faire ça bien...

par **nyafai** » 20 Oct 2006, 13:26

peut-être que je me trompe, je n'ai pas refait le calcul mais il me semble qu'on peut trouver la valeur en se ramenant d'abord à l'intégrale de Arctan(t)/t par une intégration par partie.

Ensuite il faut étudier la fonction :

et en la dérivant, trouver une équation différentielle vérifiée par G permettant de calculer explicitement G. On trouve ensuite la valeur en x=1 et donc le résultat

je vais essayer de revoir mais il me semble que j'avis déjà fait cet exo et que ca marchait comme ca.

edit: oui ca doit marcher parce que:

qui est la primitive d'une fraction rationnelle qu'on peut donc calculer explicitement :id: et ensuite on doit en déduire G(x) en primitivant

par **tize** » 20 Oct 2006, 13:41

Hé c'est pas bête du tout !
G(0)=0 et j'ai trouvé

c'est ça ?

Par contre je vois pas trop la primitive...

par **nyafai** » 20 Oct 2006, 13:46

euh désolé en fait je crois qu'on tourne en rond parce que la primitive d' arctanx/x c'est justement ce qu'on cherche...

par **tize** » 20 Oct 2006, 13:48

A...oui c'est bien ce qu'il me semblait aussi...si tu as déjà fait cet exercice et que tu le retrouve fais moi signe...
Ou si tu sais comment calculer :

n'hesite pas...
Je sais montrer que

mais avec le

...?

par **isortoq** » 20 Oct 2006, 15:53

Hum, l'intégrale de Arctan(t)/t diverge en l'infini...

par **nyafai** » 20 Oct 2006, 16:36

en effet donc ce n'est définitivement pas la bonne piste...

edit : quoi qu'on puisse l'étudier sur [0,1] d'après un précédent post

par **tize** » 20 Oct 2006, 17:17

isortoq a écrit:Hum, l'intégrale de Arctan(t)/t diverge en l'infini...

oui mais on integre de 0 à 1 avec le changement de variable x=1/t

par **Pythales** » 20 Oct 2006, 18:27

Je suis moi aussi sur 2 forums (fora?)
Voici ce que j'ai écrit sur l'autre :
Je pose

Je suis parti de la fonction

que j'intégre de

à

puis sur un cercle dont le rayon tend vers l'infini, puis de

à

puis sur un cercle de rayon tendant vers

Je trouve

mais à gauche, je trouve la valeur

c.a.d. une partie réelle et une partie imaginaire.
Les intégrales prises le long des cercles sont nulles.
Ca m'énerve, car je n'arrive pas à trouver mon erreur.
Si quelqu'un a une idée ...

par **yos** » 20 Oct 2006, 19:41

Pythales a écrit:Je suis parti de la fonction que j'intégre de à puis sur un cercle dont le rayon tend vers l'infini, puis de à puis sur un cercle de rayon tendant vers

J'ai pas regardé en détail mais il te faut, je crois, une détermination du logarithme, ce qui ne peut se faire que sur C privé d'une demi-droite d'origine O. Et ton contour d'intégration croise malencontreusement une telle demi-droite.

par **Pythales** » 20 Oct 2006, 20:50

J'ai réalisé en effet que la fonction n'est pas uniforme dans le domaine que j'ai choisi (point de branchement en 0). J'aurais du prolonger jusqu'à 0, mais dans ce cas, ça ne correspond pas à l'intégrale que je cherche.

par **tize** » 20 Oct 2006, 23:20

J'ai essayé de rentrer ma serie :

dans cette page web , c'est apparement la "constante de Catalan" :0.915965594177219015054603514932...
ayla8101 Si tu repasses par là et que tu as une solution plus "jolie"...

[EDIT:]
Je viens de trouver ceci dans la superbe Wikipedia...je crois que ça termine le débat !

par **yos** » 21 Oct 2006, 08:11

tize a écrit:J'ai essayé de rentrer ma serie : dans cette page web , c'est apparement la "constante de Catalan" :0.915965594177219015054603514932...
ayla8101 Si tu repasses par là et que tu as une solution plus "jolie"...

[EDIT:]
Je viens de trouver ceci dans la superbe Wikipedia...je crois que ça termine le débat !

C'était courru.
Mais ne sous-estimons pas les copains de classe d'Ayla8101

Intégrale impropre

Intégrale impropre

Qui est en ligne