Soit
Je cherche à trouver un équivalent simple de
J'ai essayé d'utiliser l'identité
Quelqu'un aurait-il une poste ?
Merci d'avance.
Intégrale généralisée à paramètre
2 messages
- Page 1 sur 1
Intégrale généralisée à paramètre
par zwijndrecht » 26 Sep 2024, 21:41
Bonjour,
Soit= \begin{cases} \frac{1-e^{-x}}{x} & \text{ si } x \neq 0 \\1 & \text{sinon}\end{cases})
. On vérifie facilement que 
est bien continue.
Je cherche à trouver un équivalent simple de\sin(x-t) \mathrm{dt})
quand 
.
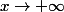
J'ai essayé d'utiliser l'identité=\sin(x)\cos(t)-\cos(x)\sin(t))
, mais ça n'a rien donné de probant...
Quelqu'un aurait-il une poste ?
Merci d'avance.
Soit
Je cherche à trouver un équivalent simple de
J'ai essayé d'utiliser l'identité
Quelqu'un aurait-il une poste ?
Merci d'avance.
Re: Intégrale généralisée à paramètre
par phyelec » 27 Sep 2024, 00:02
bonjour,
Voyez si vous arrivez à conduire le calcul en utilisant :
=\dfrac{e^{j(x-t)}-e^{-j(x-t)}}{2j})
Voyez si vous arrivez à conduire le calcul en utilisant :
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :