Bonjour à tous,
Je cherche à calculer l'intégrale I=(dx/1+sin²x) avec le changement de variable t=tan(x/2) ce qui me donne que I=(2/1+t²)dt/(1+(2t/1+t²))=2(1+t²)dt/[(t²+3+2sqrt(2))(t²+3-2sqrt(2))] mais je ne sais pas comment intégrer cela...
Merci de votre aide :)
Intégrale fraction rationelle sinus
6 messages
- Page 1 sur 1
par siger » 02 Fév 2014, 22:58
bonsoir
sauf erreur (un dimanche soir!)
on obtient
I = somme( 2dt/(1+t)^2)
sauf erreur (un dimanche soir!)
on obtient
I = somme( 2dt/(1+t)^2)
par kolorius » 02 Fév 2014, 23:06
siger a écrit:bonsoir
sauf erreur (un dimanche soir!)
on obtient
I = somme( 2dt/(1+t)^2)
Comment vous arrivez à ce résultat? Je vois pas très bien
par Ben314 » 03 Fév 2014, 11:40
Salut,
Pour
posons =\int_0^a\frac{dx}{1+\sin^{2}(x)}\)
.
Si)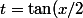
alors =\frac{2t}{1+t^2}\)
et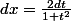 
, donc
\ =\ \int_0^{\tan(a/2)}\frac{1}{1+\left(\frac{2t}{1+t^2}\right)^2} \times \frac{2 dt}{1+t^2}\ <br /> =\ \int_0^{\tan(a/2)}\frac{2(t^2+1)}{t^4+6t^2+1}dt)
Or, comme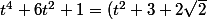(t^2+3-2\sqrt{2})\)
il existe deux constantes réelles 
et 
telles que}{t^4+6t^2+1}=\frac{\alpha}{t^2+3+2\sqrt{2}}+\frac{\beta}{t^2+3-2\sqrt{2}}\)
(décomposition en éléments simples)
Tu intégre ensuite chacun des deux morceaux en faisant un changement de variable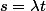
pour se ramener à du 
Bon courage...
P.S.1. Il peut être utile de remarquer que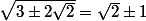
...
P.S.2. Le cahangement de variable)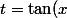
donne la solution plus simplement...
Pour
Si
Or, comme
Tu intégre ensuite chacun des deux morceaux en faisant un changement de variable
Bon courage...
P.S.1. Il peut être utile de remarquer que
P.S.2. Le cahangement de variable
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 63 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :