Integrale de sh(x)^n entre 0 et ln(1+sqrt2)

[Lostounet]

Du coup comment se fait-il que j'ai pu trouver cet équivalent (le bon résultat) plus tôt.. en disant que In-2~ In

D'autres idées pour cet équivalent? J'espère que ce sera pas 1/(V2*n) pour le coup.

[zygomatique]

salut

coup de bol ... comme le montre les interventions de samouphar ....

[Lostounet]

salut

coup de bol ... comme le montre les interventions de samouphar ....

C'est bizarre car certes c'est faux mathématiquement de sommer des équivalents, mais dans le passé il m'est souvent arrivé de trouver le bon équivalent en composant ou en sommant....

Je pense que c'est un peu plus qu'une coïncidence et qu'il devrait y avoir une CNS ou une raison profonde avec les DL par ex

Edit: ici par exemple, on peut remplaçer n'=n-2 pour voir pourquoi ça marche.

[Kolis]

Bonjour !
Il me semble que si la somme ne s'annule pas sur un voisinage on peut sommer les équivalents...

[Kolis]

Je n'ai pas pu préciser ce matin car le moteur TeX était inopérant.
Soit donc on a de limite nulle en .
Si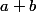 n'a pas une limite nulle en et ne s'annule pas sur un voisinage on aura
de limite 0 en .

Tout çà ne vaut RIEN.
Je pensais en fait au cas des "parties principales" par rapport à une échelle. Si dans l'échelle, lorsque 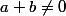alors .