Integrale Double
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 21 Nov 2019, 15:53
par mehdibj » 21 Nov 2019, 15:53
J'ai du mal à resoudre L'Integrale double suivante :

D={
\epsilonR^{2})
/

,

}
La démarche que j'ai suivit est la suivante :
soit f(x)=y-x
f(x)>0

1>y>x et
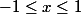
f(x)

0


et
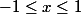
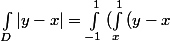dy})dx}+\int_{-1}^{1}{(\int_{x^{2}}^{x}{(x-y)dy})dx}=....=\frac{8}{3})
Ce qui est faux
(selon la correction le résultat doit étre 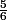 )
) ,quelqu’un peut me donner une piste ? Merci d’avance

-
arnaud32
- Membre Irrationnel
- Messages: 1982
- Enregistré le: 18 Oct 2010, 14:43
-
 par arnaud32 » 21 Nov 2019, 17:36
par arnaud32 » 21 Nov 2019, 17:36
je pense que tu devrais decouper ton domaine en 3 moreceaux
-1<x<0 et x²<y<1
0<x<1 et x²<y<x
0<x<1 et x<y<1
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 21 Nov 2019, 17:37
par pascal16 » 21 Nov 2019, 17:37
j'ai d'abord dessiné la parabole y=x² pour trouver le domaine
perso, je couperais en 3 car il me semble que tu compte avec le mauvais signe une partie :
à x fixé, on a y>x pour :
pour x<0, y varie de x² à 1
pour x>0, y varie de x à 1
à x fixé, on a y<x pour :
pour x<0 ; jamais
pour x>0, y varie de x² à x
[edit] cross post
-
mehdibj
- Membre Naturel
- Messages: 67
- Enregistré le: 15 Sep 2017, 20:04
-
 par mehdibj » 22 Nov 2019, 14:03
par mehdibj » 22 Nov 2019, 14:03
en effet j'ai considérer un seul cas pour y>x :
le calcul dans cet intervalle donne le bon résultat merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités