Intégrale double entre deux tangentes.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 19 Déc 2021, 22:27
par Pisigma » 19 Déc 2021, 22:27
lisachatroux a écrit:@Pisigma je les ai dessinées mais je n'arrive pas à voir entre quoi x et y varient c'est justement sur ce point que je n'y arrive pas

sur le dessin de
mathelot , on voit que pour un

fixé,

varie entre la courbe verte et la courbe rouge
c-à-d entre

et


-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Déc 2021, 22:38
par fatal_error » 19 Déc 2021, 22:38
Hi,
Peut être une erreur de raisonnement, mais jai l'impression que sqrt(x) et x2 sont en bij réciproque pour le domaine [0;1] et donc l'une est symétrique de l'autre par rapport à la droite d'equation y=x.
J'aurais alors tendance à calculer l'aire délimitée par y=x et y=x2, puis la doubler (vu que y=x est tjs au dessus)
L'intégrale me donne x2/2 - x3/3 soit 1/6 évaluée en 1.
Idem l'aire entre sqrt(x) et x2 est 1/3.
Beaucoup d'effort pour éviter d'intégrer sqrt(x), certes
Edit, whoopsie pas vu le post de lyceen95
la vie est une fête

-
mathelot
 par mathelot » 19 Déc 2021, 22:42
par mathelot » 19 Déc 2021, 22:42
@fatalerror : oui, mais on intègre le produit xy et pas seulement le calcul d'aire

-
fatal_error
- Membre Légendaire
- Messages: 6610
- Enregistré le: 22 Nov 2007, 12:00
-
 par fatal_error » 19 Déc 2021, 22:45
par fatal_error » 19 Déc 2021, 22:45
le produit xy
Whoops je vais marrêter là jai vraisemblalement pas les yeux en face des trous :s
la vie est une fête

-
lisachatroux
- Membre Relatif
- Messages: 155
- Enregistré le: 19 Déc 2021, 17:09
-
 par lisachatroux » 19 Déc 2021, 23:08
par lisachatroux » 19 Déc 2021, 23:08
@matelot @lyceen95 @Pisigma je vois comment vous avez fait pour trouver l'intervalle il faut que je m'intraîne en fait les deux courbes se croisent en 1 et 0 et on voit ensuite que y varie entre xcarré et racine de x, et pourquoi pas entre xcarré et x d'ailleurs car entre 0 et 1 xcarré est toujours plus petit que x ??
Du coup j'ai fait l'intégrale et ça m'a donné ça je ne sais pas si c'est juste :
http://www.noelshack.com/2021-50-7-1639 ... 230157.jpg
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 19 Déc 2021, 23:09
par lyceen95 » 19 Déc 2021, 23:09
On va revenir aux fondamentaux. Parce que là, on s'intéresse à un exercice précis, mais ce sont les fondamentaux qui manquent.
Ici tu peux procéder en 2 temps.
Tu fixes une valeur de

, par exemple
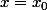
A ce niveau,

peut être vu comme une constante.
Tu calcules
 dy)
Tu as donc une fonction
 =)
... ce que tu viens de trouver.
Et tu calcules ensuite
 dx)
Ou tu peux parfaitement inverser les rôles de x et de y ... c'est symétrique.
-
lisachatroux
- Membre Relatif
- Messages: 155
- Enregistré le: 19 Déc 2021, 17:09
-
 par lisachatroux » 19 Déc 2021, 23:15
par lisachatroux » 19 Déc 2021, 23:15
Je ne comprends pas pourquoi il faut calculer d'abord selon dy puis après selon dx c'est plus facile de faire l'inverse pour intégrer non?
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 19 Déc 2021, 23:38
par lyceen95 » 19 Déc 2021, 23:38
Comme je disais dans la dernière ligne : dans l'ordre que tu veux ... mais je ne vois pas pourquoi ce serait plus facile dans l'autre ordre.
-
lisachatroux
- Membre Relatif
- Messages: 155
- Enregistré le: 19 Déc 2021, 17:09
-
 par lisachatroux » 19 Déc 2021, 23:44
par lisachatroux » 19 Déc 2021, 23:44
Du coup est-ce que tu peux me dire si ce que j'ai fait est juste ?
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 19 Déc 2021, 23:47
par Pisigma » 19 Déc 2021, 23:47
attention!!
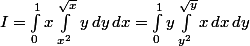
dans la 2e intégrale, tu fixes

et

varie entre la courbe rouge et la courbe verte soit entre
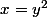
et
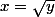
-
mathelot
 par mathelot » 20 Déc 2021, 00:45
par mathelot » 20 Déc 2021, 00:45
-
lisachatroux
- Membre Relatif
- Messages: 155
- Enregistré le: 19 Déc 2021, 17:09
-
 par lisachatroux » 20 Déc 2021, 12:03
par lisachatroux » 20 Déc 2021, 12:03
J'avais trouvé 1/6 merci @mathelot !
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 20 Déc 2021, 20:51
par tournesol » 20 Déc 2021, 20:51
Lisa , tu dois bien comprendre comment ton domaine d'intégration est décrit :
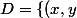 | x\in [0;1]ETy\in[x^2 , \sqrt{x}]\}=\{(x,y) | 0\le x\le 1ETx^2 \le y\le \sqrt{x}]\}= y\in\cup_{x\in [0;1]}\{x\}\times [x^2 , \sqrt{x}])
Modifié en dernier par
tournesol le 21 Déc 2021, 02:36, modifié 1 fois.
-
lyceen95
- Membre Complexe
- Messages: 2263
- Enregistré le: 14 Juin 2019, 23:42
-
 par lyceen95 » 20 Déc 2021, 22:27
par lyceen95 » 20 Déc 2021, 22:27
A chaque fois que je lis cette discussion, ça me titille, alors on va crever l'abcès. Pourquoi le titre de la discussion parle-t-il de tangentes ? Il n'y a pas de tangente dans cet exercice.
-
tournesol
- Membre Irrationnel
- Messages: 1509
- Enregistré le: 01 Mar 2019, 18:31
-
 par tournesol » 21 Déc 2021, 02:39
par tournesol » 21 Déc 2021, 02:39
Bien vu lyceen95 .
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités