Integrale double ; changement de variable

[MacErmite2]

Bonjour à tous,

J'aimerais intégrer cette expression :


En posant :



En posant : et cela permet de "passer" en coordonnées polaires. Cependant je m'y perds pour trouver le domaine d'intégration avec ce changement de variable.
Pouvez-vous m'aider ?
Merci.

[Ben314]

Salut,
Je sais pas trop ce que tu compte faire comme calcul :
- Si tu espère avoir une "valeur explicite" de en fonction de à l'aide uniquement de "fonctions élémentaires" (log, exp, etc, etc...) alors il est connu comme le loup blanc qu'il n'y en a pas.
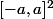
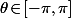
- Si tu veut juste savoir s'il est possible de "paramétrer" le carré en terme de coordonnées polaire alors la réponse est évidement oui : pour décrire les tels que tu peut par exemple prendre puis (mais ça ne te mènera pas à grand chose comme calculs)
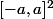
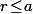
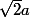
- Sinon, si tu veut un encadrement de en partant sur ce principe, il te suffit évidement de dire que le carré contient le disque de centre (0,0) et de rayon (correspondant à l'unique condition ) et est contenu dans celui de centre (0,0) et de rayon (correspondant à l'unique condition ).
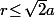
Tu en déduit immédiatement un majorant et un minorant simple de .

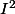
[MacErmite2]

Mince alors,

Ce genre d'exercice remonte, pour moi, à une époque ou Microsoft sortait Windows 3.1 !! De plus je viens de découvrir le changement de variables en passant par une matrice Jacobienne ...

Je cherche sur le net des vidéos tutos, avec beaucoup de pédagogie, pour comprendre le pourquoi du comment.

[Pythales]

Le changement de variable n'est intéressant que pour .

Sinon, la fonction s'appelle erf(x). Il y a des tables pour la calculer.

[MacErmite2]

En fait je cherche à connaître la valeur de a pour I connu ...

[Ben314]

Ca ne change rien au problème : on ne sait exprimer ni la fonction directe, ni sa réciproque à l'aide des "fonctions usuelles" (exp, ln, trigo, etc...).
Pendant longtemps, on a effectivement utilisé des tables pour trouver les valeurs approximatives de cette fonction (et de sa réciproque) et il continue à y en avoir à pas mal d'endroit.
Mais d'un autre coté, on utilisait aussi des tables pour toutes les fonctions transcendantes élémentaires, c'est à dire les logarithmes, exponentielles et fonctions trigo. Lors de l'apparition des premiers calculateurs (puis calculatrices), assez rapidement on a implémenté dessus des touches log, exp et trigo (donnant évidement des valeurs approximatives) et c'est devenu "les fonctions usuelles".
Au départ, on a implémenté que celle là parce que c'était considéré comme suffisant dans la grande majorité des cas et que sur n'importe quelle ordi. ou calculette programmable, on pouvait à sa guise programmer d'autres fonctions.
A l'heure actuelle, presque tout les programmes d'ordi. faisant un tant soit peu de calcul scientifique (*) et pas mal de calculettes possèdent une touche correspondant à cette fonction donc les fameuses "tables de valeur" sont en train de tomber dans l'oubli comme les tables de log de nos grand parents.

(*) Pour donner un exemple au pif., sous Open Office la fonction est nommée GAUSS et sa bijection réciproque est nomméeLOI.NORMALE.STANDARD.INVERSE.

[MacErmite2]

Merci pour vos participations.