Integrale changement de variable

[p0805289]

Bonjour j'aurais besoin de votre aide pour faire l'integrale de cette fonction , arcsin(2x/1+x²) on me dit que je peux mettre x=tan(u)
j'ai trouvé ça l'intergale de arcsin(2tan(u)/1+tan²)
on sait que tan(2u)=2tan(u)/1-tan²(u) mais ça marche pas .
si vous avez des idées je vous remercie d'avance..

[Ericovitchi]

2 tan u / (1+ tan² u ) = sin 2u

[mathelot]

Bonjour,

l'exercice est très confusant. A mon avis, le changement de variable
proposé x=tan(u) permet de simplifier l'intégrande (la fonction à intégrer)
mais en gardant, au final, la même variable d'intégration x !!

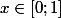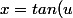par exemple si , on pose bijectivement avec

et on trouve f(x)=2arctan(x)

mais des primitives de arctan(x)dx, on en connait , en intégrant par parties.


ce que je veux dire, c'est que si l'on avait à primitiver:

on simplifierait en

içi ton changement de variable est du même ordre.
C'est juste une réécriture de formule.

[mathelot]

rebonjour,

j'ai réécrit l'énoncé à ma sauce
1° simplification

soit
en posant x=tan(u) , simplifier l'expression de f sur les intervalles

et


f(x)=2arctan(x) si 0 = 1

2° primitive de 2arctan()

en intégrant par partie, indiquer une primitive de 2arctan()

2x arctan(x)- ln(1+x2)

3° primitive de f()

en déduire

[Ericovitchi]

moi je ne vois rien de spécialement troublant dans le fait de poser x= tan u

arc sin (2x/(1+x²)) = 2u et dx = (1+tan ²u)du

donc ça revient à intégrer u tan²u .Pour faire ça le plus simple est une intégration par partie en l'écrivant -u sinu d(1/cosu)

[mathelot]

Finalement, si , j'obtiens:

si
si

arc sin (2x/(1+x²)) = 2u

celle là est valide si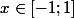

s'intégre difficilement. A mon humble avis, vous vous êtes fait tous les deux prendre à ce piège diabolique. :zen:
Le changement de variable ne sert qu'à simplifier la formule de l'intégrande
et n'est pas utilisé comme le C1-difféomorphisme habituel.
On reste en variable x, même après changement de variable x=tan(u)

On trouve effectivement 2u=2arctan(x) dans 1 cas sur 2.