Intégrale bornée, fonction identiquement nulle
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 15:42
par Nightmare » 17 Mai 2009, 15:42
Salut à tous :happy3:
On m'a fait découvrir aujourd'hui un résultat surprenant que je n'arrive pas à démontrer.
On connait tous le résultat :
Si f est continue sur [1,2] (on pourrait prendre n'importe quel segment )et telle que pour tout n naturel
dx=0)
alors

(trivial en approchant par exemple f par des polynômes)
Il semblerait que le résultat suivant soit vrai :
Si f continue sur [1,2] et si la suite
dx\)_{n\in \mathbb{N}})
est bornée alors

Une idée de démonstration?
Merci à vous :happy3:
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 17 Mai 2009, 15:48
par Maks » 17 Mai 2009, 15:48
Waow ... Marrant ce truc ... De là à avoir une idée de démonstration dans l'instant ...
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 16:27
par Nightmare » 17 Mai 2009, 16:27
Une idée :
On considère la fonction entière
=\Bigint_{1}^{2} e^{zt}f(t)dt)
On a
=\Bigint_{1}^{2} t^{n}f(t)dt)
Il s'agirait donc de montrer que la dérivée n-ème en 0 est toujours nulle.
Avec un développement en série entière de exp on montre que F est bornée sur

.
Mon idée serait de montrer qu'elle l'est en fait sur
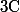
ce qui permettrait de conclure par le théorème de Liouville qu'elle est constante !
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 17 Mai 2009, 16:35
par Maks » 17 Mai 2009, 16:35
Cela dépasse mes connaissances ... Que stipule le théorème de Liouville, s'il-te-plaît ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 16:45
par Nightmare » 17 Mai 2009, 16:45
Il stipule que toute fonction entière (ie holomorphe sur
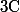
) et bornée est constante.
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 17 Mai 2009, 16:49
par Maks » 17 Mai 2009, 16:49
Merci. Cependant, je ne sais pas ce qu'est une fonction holomorphe. J'en ai déjà entendu parler, mais jamais rencontré, ni en cours, ni en exercice. Je regarderai ça quand j'aurai le temps.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 16:51
par Nightmare » 17 Mai 2009, 16:51
holomorphe = dérivable au sens complexe
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 17 Mai 2009, 16:56
par Maks » 17 Mai 2009, 16:56
= je n'ai pas vu ... malheuresement ... C'est vrai que dériver dans les complexes ... comment définir cela ? Dans les réels, on assimile la dérivation au taux de variation, lorsque l'on se déplace un petit peu sur la droite réelle ... Mais dans les complexes ... On se déplace dans le plan complexe ?
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 17:01
par Nightmare » 17 Mai 2009, 17:01
Ben pareil, avec un taux d'accroissement et une limite, sauf que dans le cas réel on a que deux manières d'approcher un point, dans le cas complexe une infinité.
-
Maks
- Membre Relatif
- Messages: 474
- Enregistré le: 14 Mai 2009, 21:03
-
 par Maks » 17 Mai 2009, 17:03
par Maks » 17 Mai 2009, 17:03
Oui, justement, comment paramètre-t-on la direction d'approche ? Et puis s'approche-t-on toujours via une droite ? C'est une sorte de dérivation par rapport à un vecteur ?

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 17 Mai 2009, 18:22
par leon1789 » 17 Mai 2009, 18:22
Nightmare a écrit:Une idée de démonstration?
Une idée : si f est continue sur un intervalle [a,b] avec

, et
 \neq 0)
, alors
.x^n\ dx)
équivaut à
.b^{n+1}/n)
quand n tend vers l'infini (ce qui est loin d'être borné :id:)
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 17 Mai 2009, 18:47
par MathMoiCa » 17 Mai 2009, 18:47
Salut,
En définissant le produit scalaire suivant :
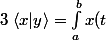y(t) ~dt)
, on peut prouver que ta relation est vraie pour toute fonction polynômiale. Car
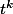
appartient à la base de P[X], l'ensemble des polynômes.
Et après on utilise la densité de l'ensemble des polynômes dans l'ensemble des fonctions continues sur un compact (pas sûre pour le compact), en utilisant le th. de Weierstrass par exemple.
Sinon, au lieu de passer par le produit scalaire, on peut carrément écrire
=\sum_{k=0}^n a_k x^k)
et ça se montre...
M.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 20:30
par Nightmare » 17 Mai 2009, 20:30
leon1789 a écrit:Une idée : si f est continue sur un intervalle [a,b] avec

, et
 \neq 0)
, alors
.x^n\ dx)
équivaut à
.b^{n+1}/n)
quand n tend vers l'infini (ce qui est loin d'être borné :id:)
Ok, l'équivalent n'est pas difficile à montrer. Belle méthode !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 17 Mai 2009, 20:31
par Nightmare » 17 Mai 2009, 20:31
MathMoiCa a écrit:Salut,
En définissant le produit scalaire suivant :
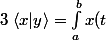y(t) ~dt)
, on peut prouver que ta relation est vraie pour toute fonction polynômiale. Car
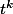
appartient à la base de P[X], l'ensemble des polynômes.
Et après on utilise la densité de l'ensemble des polynômes dans l'ensemble des fonctions continues sur un compact (pas sûre pour le compact), en utilisant le th. de Weierstrass par exemple.
Sinon, au lieu de passer par le produit scalaire, on peut carrément écrire
=\sum_{k=0}^n a_k x^k)
et ça se montre...
M.
Comment montres-tu que c'est vrai pour les polynômes?
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 18 Mai 2009, 07:27
par MathMoiCa » 18 Mai 2009, 07:27
Tu te places dans l'espace des polynômes de degré n P[X] (j'sais pas comment on appelle ça exactement). La base canonique est
On considère f polynôme de degré n.
D'après l'énoncé, f est orthogonal à tout élément de la base. Donc est orthogonal à lui-même.
Or par définition du produit scalaire, ça signifie que

Et après on applique Weierstrass.
M.
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 18 Mai 2009, 07:34
par MathMoiCa » 18 Mai 2009, 07:34
Sinon, comme proposé :
=\sum_{k=0}^n a_kx^k)
Donc
t^k ~dt=0 \hfill \\<br />\Rightarrow \sum_{k=0}^n a_k \int_a^b f(t)t^k ~dt=0 \hfill \\<br />\Rightarrow \int_a^b f(t)\sum_{k=0}^n a_kt^k ~dt=0 \hfill \\<br />\Rightarrow \int_a^b f^2(t) ~dt=0 \hfill \\<br />\Rightarrow f\equiv 0 \hfill <br />\end{gather})
(celle-là, c'est qqn d'autre qui l'a trouvée)
M.
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 18 Mai 2009, 13:41
par Nightmare » 18 Mai 2009, 13:41
Mathmoica > Ok on s'est mal compris !
Tu pars de l'énoncé
dt=0)
qui n'est pas celui traité dans le topic :lol3:
Il faut partir de l'hypothèse
dt) bornée
bornée !
-
MathMoiCa
- Membre Rationnel
- Messages: 518
- Enregistré le: 20 Jan 2008, 12:57
-
 par MathMoiCa » 18 Mai 2009, 19:23
par MathMoiCa » 18 Mai 2009, 19:23
Ah bawi forcément, j'ai mal lu :dodo:
Désolée
M.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
alors
(trivial en approchant par exemple f par des polynômes)
est bornée alors
