Intégrale en arcsinus

par **le fouineur** » 30 Juin 2007, 15:52

Bonjour à tous,

Je suis bloqué depuis longtemps avec cette intégrale;

On propose dans l'énoncé le changement de variable:

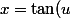Sachant que:

En l'appliquant à mon intégrale, je trouve après simplification:

Mais en prenant l'intégrale de 0 à 1 je m'aperçois que ma primitive est fausse...Ou est donc l'erreur et comment faut-il procéder pour arriver à un résultat juste?

Merci de m'aider cordialement le fouineur

par **achille** » 30 Juin 2007, 16:12

salut tu calcules l'intégrale entre 0 et 1 pour la variable x ou u ?? Juste pour vérifier les calcules avec toi :we:

par **Joker62** » 30 Juin 2007, 16:12

0..1 c'est les bornes de l'intégrale initiale ???

Si oui, faut pas oublier de changer les bornes après le changement variable

x = 0 = tan(u) <=> u = 0
x = 1 = tan(u) <=> u = pi/4

Trop tard :D

par **achille** » 30 Juin 2007, 16:32

hehe oui bonne remarque :zen:

par **le fouineur** » 30 Juin 2007, 17:05

Merci à tous ceux qui ont apporté leur contribution,

J' avais oublié de modifier les bornes suite au changement de variable....

L'intégrale vaut:

Cordialement le fouineur

par **achille** » 30 Juin 2007, 17:44

:doh: heureux pour toi l'ami...

Intégrale en arcsinus

Intégrale en arcsinus

Qui est en ligne