Intégrale absolument convergente
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 12:48
par chelsea-asm » 11 Nov 2012, 12:48
Bonjour,
Je cherche à prouver que
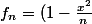^n)
est intégrable pour tout
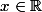
J'ai montré précédemment que
^n \leq e^{u})
si

J'ai également montré que

est convergente.
Le but est donc de montrer que
^n|dx)
est convergente.
Or,
^n \leq e^{-x^2})
si

c'est à dire si

c'est à dire

Ainsi
^n|dx \leq \int\limits_{0}^{+\infty} e^{-x^2}\, \mathrm dx)
Donc
^n|dx)
converge.
Puis-je utiliser la parité de la fonction exp pour montrer que
^n|dx)
converge ?
Et comment l'élargir à l'infini ? En utilisant un point a qui tend vers + ou - l'infini ? Il faudrait trouver une primitive ce qui s'avère plutôt compliqué...
Merci pour vos commentaires et votre aide.
Cordialement,
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Nov 2012, 13:21
par Le_chat » 11 Nov 2012, 13:21
Ce truc là ne va pas être intégrable sur R, vu que selon la parité de n ça tend vers plus ou moins l'infini selon x ( c'est un polynôme, au fond).
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 13:51
par chelsea-asm » 11 Nov 2012, 13:51
Oui mais puisqu'il s'agit d'une valeur absolue, puisqu'on cherche à ce que ce soit absolument convergent, que ça tende vers + ou - l'infini en valeur absolue cela tend vers + l'infini non ?
D'où la question du sujet : Montrer que chaque fonction

est intégrable sur

-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Nov 2012, 15:53
par Le_chat » 11 Nov 2012, 15:53
Une fonction qui tend vers plus l'infini en l'infini en valeur absolue ne risque pas d'être intégrable.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 17:02
par chelsea-asm » 11 Nov 2012, 17:02
Le_chat a écrit:Une fonction qui tend vers plus l'infini en l'infini en valeur absolue ne risque pas d'être intégrable.
Ben oui je vois, mais alors il est impossible de répondre à cette question ?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Nov 2012, 17:07
par Le_chat » 11 Nov 2012, 17:07
Si, tu peux dire que c'est faux ^^
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 17:32
par chelsea-asm » 11 Nov 2012, 17:32
Le_chat a écrit:Si, tu peux dire que c'est faux ^^
Mdr ^^ ok merci beaucoup

-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 18:07
par chelsea-asm » 11 Nov 2012, 18:07
Mais si je rajoute que
 = (1-\frac{x^2}{n})^n)
pour

] et
=0)
sinon ?
-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Nov 2012, 18:20
par Le_chat » 11 Nov 2012, 18:20
Ben là c'est à support compact et continu par morceau donc intégrable.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 18:40
par chelsea-asm » 11 Nov 2012, 18:40
Le_chat a écrit:Ben là c'est à support compact et continu par morceau donc intégrable.
Ok merci, dans ce cas, mon premier message est-il juste ? Et comment je fais pour prolonger sur l'infini après ?
Merci encore

-
Le_chat
- Membre Rationnel
- Messages: 938
- Enregistré le: 10 Juin 2009, 12:59
-
 par Le_chat » 11 Nov 2012, 18:42
par Le_chat » 11 Nov 2012, 18:42
Ben tu dis que l'integrale de |fn| sur R c'est l'integrale de |fn| sur [-n,n] donc l'integrale converge.
-
chelsea-asm
- Membre Relatif
- Messages: 289
- Enregistré le: 08 Fév 2009, 16:13
-
 par chelsea-asm » 11 Nov 2012, 19:25
par chelsea-asm » 11 Nov 2012, 19:25
Ben oui mais comme j'ai fait de
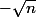
à
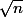
(c'est peut-être faux ma démarche) mais comment je prolonge à -n,n alors ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 53 invités
