Intégrale abélienne
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 11 Aoû 2022, 14:19
par lefouineur » 11 Aoû 2022, 14:19
Bonjour Pisigma et merci pour ta réponse rapide,
J'ai corrigé l'intégrale, il vient:
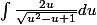
et
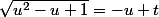
on élève au carré
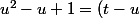^2)
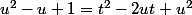
on simplifie
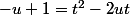
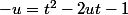
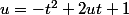
d'oû
dt)
Est-ce-que c'est bon jusque là? Que faut-il faire ensuite?
Merci de me répondre cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 11 Aoû 2022, 14:35
par Pisigma » 11 Aoû 2022, 14:35
lefouineur a écrit:J'ai corrigé l'intégrale, il vient:
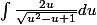
petite coquille ici
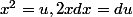
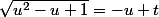
on élève au carré
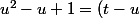^2)
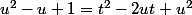
on simplifie
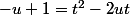 ici il faut regrouper les u dans le 1er membre
ici il faut regrouper les u dans le 1er membre de façon à écrire
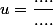
ensuite il faut calculer
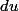
et remplacer dans l'équation de départ
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 12 Aoû 2022, 16:14
par lefouineur » 12 Aoû 2022, 16:14
Bonjour Pisigma et merci pour ta réponse rapide,
Je ne comprends pas bien la coquille dans l'intégrale, c'est bien:
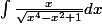
dont il s'agit? pourrais-tu me détailler le calcul(changement de variable (x^2=u))
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 12 Aoû 2022, 16:38
par Pisigma » 12 Aoû 2022, 16:38
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 12 Aoû 2022, 19:09
par lefouineur » 12 Aoû 2022, 19:09
Merci pour ta correction, Pisigma.
J'ai fait le calcul de u:
-u+1=t²-2ut
-u+2ut=t²-1
u(-1+2t)=t²-1
d'oû
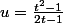
et
}{(2t-1)^2}dt)
ce qui donne dans l'intégrale en u:
^2}dt)
(après simplifications)
Qu'en penses-tu?
Cordialement lefouineur
Modifié en dernier par
lefouineur le 12 Aoû 2022, 21:07, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 12 Aoû 2022, 19:28
par Pisigma » 12 Aoû 2022, 19:28
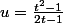
et
}{(2t-1)^2}dt) OK
OKaprès c'est faux
montre un peu ton développement
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 13 Aoû 2022, 06:21
par Pisigma » 13 Aoû 2022, 06:21
tu devrais trouver
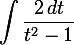
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 13 Aoû 2022, 09:51
par lefouineur » 13 Aoû 2022, 09:51
Bonjour Pisigma et merci pour ta réponse,
J'aimerai bien te poster mes calculs mais il sont trop lourds pour être écrits en latex (écriture que je ne maîtrise pas). J'ai réécrit l'intégrale en u en intégrale en t donc en remplaçant u et du par leur valeur. Mais je ne vois aucune simplification apparaitre....Je suis vraiment bloqué à cette étape.
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 13 Aoû 2022, 10:16
par Pisigma » 13 Aoû 2022, 10:16
n'as tu pas oublié de remplacer le radical?
il y a pas mal de simplifications dans le coefficient de
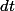
tu peux poster ton manuscrit sur un hébergeur d'images si c'est plus facile pour toi
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 13 Aoû 2022, 14:05
par lefouineur » 13 Aoû 2022, 14:05
Pisigma,
Je te poste ce que j'ai fait, je ne sais pas comment on poste des photos.
}{(2t-1)^2}}{\sqrt{\frac{(t^2-1)^2}{(2t-1)^2}-\frac{t^2-1}{2t-1}+\frac{2t-1}{2t-1}}}dt)
Cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 13 Aoû 2022, 14:46
par Pisigma » 13 Aoû 2022, 14:46
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 14 Aoû 2022, 15:31
par lefouineur » 14 Aoû 2022, 15:31
Bonjour Pisigma et merci pour ta réponse rapide
Je reprends:
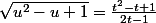
}{(2t-1)^2})
donc
}{(2t-1)^2}}{\frac{t^2-t+1}{2t-1}}dt)
finalement il reste:
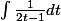
Ou est l'erreur?
Indiques-moi comment faire en latex des formules de taille normale, merci d'avance.
Cordialement lefouineur
Modifié en dernier par
lefouineur le 14 Aoû 2022, 17:17, modifié 2 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 14 Aoû 2022, 15:43
par Pisigma » 14 Aoû 2022, 15:43
tu as oublié de multiplier par u au dénominateur
Indiques-moi comment faire en latex des formules de taille normale
qu'entends-tu par taille normale?
petite confusion de ma part: ma remarque porte sur la 2e primitive évidemment ;pour la 1ère il n'y a pas de u donc ta réponse est juste mais 2t-i est plutôt 2t-1 mais OK, j'ai compris
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 15 Aoû 2022, 10:39
par lefouineur » 15 Aoû 2022, 10:39
Bonjour Pisigma et merci pour ta réponse,
Ce que j'entends par taille normale est lisible et non rikiki comme le sont les intégrales que je poste sur le forum!
J'ai essayé de m'attaquer à la seconde intégrale mais ce que j'obtiens n'est pas convaincant:
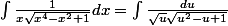
Pourrais-tu m'éclairer? cordialement lefouineur
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 15 Aoû 2022, 11:04
par Pisigma » 15 Aoû 2022, 11:04

-
WillyCagnes
- Membre Transcendant
- Messages: 3753
- Enregistré le: 21 Sep 2013, 19:58
-
 par WillyCagnes » 15 Aoû 2022, 11:36
par WillyCagnes » 15 Aoû 2022, 11:36
bonjour
x²=u
il manque la racine de U au dénominateur au lieu de u
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 15 Aoû 2022, 12:07
par Pisigma » 15 Aoû 2022, 12:07
Bonjour WillyCagnes
tu as lu trop vite!
WillyCagnes a écrit:bonjour
x²=u
il manque la racine de U au dénominateur au lieu de u
non c'est correct, car au dénominateur c'est
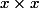
soit
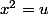
(il faut multiplier

par celui provenant de
)
Pisigma a écrit: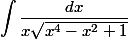
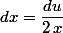
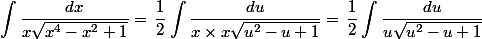
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 15 Aoû 2022, 20:42
par lefouineur » 15 Aoû 2022, 20:42
Merci Pisigma pour ta réponse rapide, la réponse pour la première intégrale est donc:
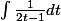
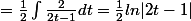
et pour la seconde:
^\frac{1}{2}=ln\sqrt{{\frac{|t-1|}{|t+1|}}})
A présent il faut revenir en u puis en x.... Pas évident vu la complexité des transformations utilisées.
Cordialement lefouineur
Modifié en dernier par
lefouineur le 16 Aoû 2022, 17:14, modifié 1 fois.
-
Pisigma
- Habitué(e)
- Messages: 3134
- Enregistré le: 21 Déc 2014, 23:38
-
 par Pisigma » 15 Aoû 2022, 21:13
par Pisigma » 15 Aoû 2022, 21:13
la 2 primitive est fausse; voir mon post du 13 août à 06h21
attention il manque les modules aux
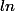
-
lefouineur
- Membre Naturel
- Messages: 66
- Enregistré le: 02 Fév 2022, 15:45
-
 par lefouineur » 15 Aoû 2022, 21:25
par lefouineur » 15 Aoû 2022, 21:25
Justement, d'oû vient le 2 au numérateur?
Cordialement lefouineur
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 33 invités
petite coquille ici
on élève au carré
on simplifie
ici il faut regrouper les u dans le 1er membre de façon à écrire
ensuite il faut calculer
et remplacer dans l'équation de départ