Integrabilité d'une fonction

par **amk** » 25 Fév 2006, 23:07

Slt,

Soit y une variable réelle positive

A première vue ça a l'air d'une intégrale de troisième éspèce mais il ya une singularité éliminable en 0 qui nous ramène à une intégrale de 1ère éspèce :
je décompose l'intégrale :

comment je pourrais conclure sur la convergence de l'intégrale figurant dans le deuxième terme ?

Merci

par **abcd22** » 25 Fév 2006, 23:35

Bonsoir !
En prenant un équivalent de la fonction sous l'intégrale au voisinage de l'infini on voit qu'elle est intégrable.

par **amk** » 25 Fév 2006, 23:50

en fait je viens de revoir l'énoncé et la borne sup était 1 et pas l'infini , enfin le raisonement est pareil j'imagine.

par **abcd22** » 25 Fév 2006, 23:57

Oui au voisinage de 1 ça marche avec un équivalent, et en 0 avec le prolongement par continuité.

par **amk** » 26 Fév 2006, 17:24

Prolongement par continuité ? c'est un équivalent en 0 aussi non ? (

)
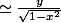
Pourquoi as tu parlé de prolongement en 0 et pas en 1 ?

par **abcd22** » 26 Fév 2006, 17:43

Parce que quand x tend vers 0 la fonction tend vers y, c'est une limite finie donc on peut la prolonger par continuité et elle est intégrable au voisinage de 0 (mais ça marche aussi en prenant un équivalent). En 1 la limite est infinie donc on ne peut pas faire de prolongement par continuité.

par **amk** » 26 Fév 2006, 18:05

Merci pour les explications :)

Integrabilité d'une fonction

integrabilité d'une fonction

Qui est en ligne