Injectivité d'une fonction R^3

[mikogh19]

Bonjour,
Ca paraitra surement simple pour certains d'entre vous, mais je peine à montrer que f est injective sur R^3 pour prouver le difféomorphisme global. J'ai essayé de poser f(x1,y1,z1) = f(x2,y2,z2) mais sans résultat. Merci infiniment !
La fonction est la suivante:
f(x,y,z) = ( e^2y + e^2z , e^2x - e^2z , x - y )

[mathelot]

Hi,
je la trouve injective mais pas surjective

[mikogh19]

Hi,
je la trouve injective mais pas surjective

Bonsoir,
On m’a demandé de montrer que c’était un diffeo de R^3 sur f(R^3) à determiner donc l’ensemble image n’est pas R^3 tout entier

[mathelot]

Bonsoir,
d'accord.

Soient les réels x,y,z,u,v,w.
posons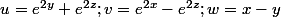

si l'on arrive à calculer x,y,z en fonction de u,v,w,c'est gagné, une image aura exactement un unique antécédent.

Posons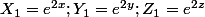
Il s'agit de calculer

il vient:



Calculer (en fonction de u,v,w) ...

[mathelot]

les deux premières égalités forment un système de Cramer d'inconnues et :










en revenant aux coordonnées x;y;z:



Toute image , par f, possède un antécédent unique. f est donc injective.

[mikogh19]

Merci beaucoup, désolé de ne pas avoir pu répondre plus tot. Ici ce n’est pas plutot la surjectivité qui est montrée ?

[mathelot]

Pour calculer l'antécédent de (u,v,w) ,il faut, au cours du calcul, que 0<u+v et 0<ue^{2w}-v,ce qui donne des contraintes [b]pour définir f(R).[/b] f n'est pas surjective.
On démontre l'injectivité de f (les images ont un unique antécédent que l'on calcule) et en plus on découvre des conditions définissant f(R)