Injection

par **Taylor 07** » 08 Juil 2010, 19:25

Soit f : N vers N une application injective, telle que pour tout n de N, f(n)
Moi je me suis dit que :

Soit n et n' dans N alors f(n)=f(n') implique que n=n' mais après ??

par **Finrod** » 08 Juil 2010, 19:31

La restriction à tout sous ensemble fini de N de la forme [0,n] est bien définie car f(n)
Tu as un truc injectif sur un ensemble fini.... donc ....

edit: prouve seulement que c'est bijectif. Reste à montrer bijection croissante dans N = Identité.

par **Taylor 07** » 08 Juil 2010, 19:34

Les nombres sont "eux même" ????

par **girdav** » 08 Juil 2010, 19:34

Bonjour,
on peut raisonner par récurrence.

par l'hypothèse et comme

est un entier, cela permet de fixer se valeur.
Si pour

on a

, il faut montrer que

. On a déjà que

.
Vois-tu pourquoi la dernière inégalité ne peut être est stricte?
Édit... (c'est normal que tu ne le voyais pas puisque c'était faux)

par **Taylor 07** » 08 Juil 2010, 19:37

Franchement non

par **Ben314** » 08 Juil 2010, 23:01

Un petit rappel : dire que f est injective signifie que, pour tout a,b, si f(a)=f(b) alors a=b. Par contraposition, cela signifie aussi que, si a est différent de b alors f(a) est différent de f(b).

Vu l'hypothèse de récurrence faite, on a f(0)=0, f(1)=1, f(2)=2, ... , f(n)=n.
Comme f est supposée injective et que n+1 est différent de 0, on a f(n+1) différent de f(0)=0.
Mais n+1 est aussi différent de 1 donc f(n+1) différent de f(1)=1 ... etc etc
Et vu que f(n+1)=<n+1, ben y'a pas trop guére le choix...

par **Taylor 07** » 09 Juil 2010, 00:30

girdav a écrit:Bonjour,
on peut raisonner par récurrence.
par l'hypothèse et comme est un entier, cela permet de fixer se valeur.
Si pour on a , il faut montrer que . On a déjà que .
Vois-tu pourquoi la dernière inégalité ne peut être est stricte?
Édit... (c'est normal que tu ne le voyais pas puisque c'était faux)

Comment ça

, c'est pas le contraire ?

par **Finrod** » 09 Juil 2010, 08:13

Taylor 07 a écrit:Comment ça , c'est pas le contraire ?

Tu as les deux.

f(0) est positif car c'est une fonction de N dans N (et non dans Z)

L'autre inégalité est donné en hyp, oui.

par **girdav** » 09 Juil 2010, 09:08

Un petit truc, qui n'a rien à voir avec le problème : pourquoi dans la citation d'un message le "\leq" apparaît-il comme un "<"?

par **Taylor 07** » 09 Juil 2010, 09:13

C'est pour dire inférieur ou égal (surtout le égal)

par **girdav** » 09 Juil 2010, 09:30

Taylor 07 a écrit:C'est pour dire inférieur ou égal (surtout le égal)

Je sais, mais le code

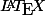
est par exemple f(n)\leq n et il est affiché un < (mais seulement dans la citation, pas dans le message original).

par **Finrod** » 09 Juil 2010, 11:40

What ?

Dans la citation que j'ai fait au message 8, le \leq est resté \leq.

Le copier collé marche jamais sur les formules Tex mais les citations, jamais vu de problème.

Injection

Injection

Qui est en ligne