Informatique python

[Melio]

Bonjour a tous j'ai un algo à rendre pour vendredi et je ne sais vraiment pas par où commencer...
Je vous met ici le travail demandé: " Etant donnée une liste de point P_1,...,P_N et K autre points Q_1,...,Q_K, l'algo renvoie K listes, la i-ème liste étant celles des points P_j telle que la plus petite distance entre les P_j et Q_p est celle obtenue avec p=i. "

Voila merci beaucoup à ceux qui prendront le temps de m'aider

[GaBuZoMeu]

Tu peux commencer par un sous-objectif plus simple : étant donné un point P et une liste de points Q_1,...,Q_K, renvoyer la plus petite distance entre P et les Q_p.

[tournesol]

Je ne comprens pas la question .
Quel est le role du paramètre p ?
La liste i est elle celle du(ou des ) points P qui est (sont ) le (les) plus proche(s) de Qi ?

[GaBuZoMeu]

Ça me semble assez clair, même si ce n'est pas très bien formulé.
La liste n°i est la liste des P_j tels que le minimum de dist(P_j,Q_p) pour p=1,...K soit égal à dist(P_j,Q_i).
C'est pourquoi je suggère d'écrire dans un premier temps une procédure qui calcule pour un point P et une liste [Q_1,...,Q_K] le minimum de dist(P,Q_p) pour p=1,...K.

[tournesol]

Merci GaBuZoMeu
Afin de savoir si j'ai bien compris je te pose le bp en termes de theorie des ensembles .
Soit G la correspondance definie sur par ensemble des points de les plus proches de 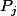, ie qui réalisent
Alors pour tout i dans {1,k} ,

[GaBuZoMeu]

Oui, si tu préfères formuler les choses de manière plus compliquée.

[tournesol]

Plus compliqué , certes mais ma formulation permet une approche matricielle tres simple de ce pb :
La matrice D des distances entre points
La matrice M binaire indicatrice des minimums par colonnes
Li est alors évidente .

[GaBuZoMeu]

Tu voulais sans doute écrire .
Le problème ici est celui d'écrire une procédure python. Autant éviter les matrices qui nécessitent l'utilisation de numpy,

[tournesol]

Merci de corriger , je voulais dire d(Qi , Pj) , i étant l'indice de ligne .
Je ne sais pas programmer en python .
Je saurais implémenter un programme matriciel dans casio graph 35 + .

[lyceen95]

Personnellement, j'ai besoin de beaucoup me concentrer pour comprendre la question.
Je pense que le problème est le même pour Melio.

Donc la première chose à faire, c'est de faire tout le nécessaire pour bien comprendre la question.
Réécrire la question, un peu comme GBZM l'a fait dans son premier message.
Très certainement, c'est utile de faire un dessin avec 4 ou 5 points dans chacun des 2 ensembles, et chercher à la main quelles sont ces fameuses listes de points.

Ensuite, on pourra parler algorithme. Mais d'abord, il faut savoir résoudre cette question 'sur un dessin'.

[LB2]

Bonjour,

autrement dit, il faut déjà savoir l'écrire en pseudo code avant de l'implémenter en Python

[tournesol]

@lycéen95 Pour établir ma formulation , j'ai fait un dessin pour comprendre .

[GaBuZoMeu]

On fonctionne différemment. Perso, je trouve qu'un dessin n'apporte absolument rien.

Je répète que la liste n°i est la liste des P_j tels que le minimum de dist(P_j,Q_p) pour p=1,...K soit égal à dist(P_j,Q_i).
Si on écrit dans un premier temps une procédure qui calcule, pour un point P et une liste [Q_1,...,Q_K], le minimum de dist(P,Q_p) pour p=1,...K, alors il est clair comment écrire une procédure qui fabrique la liste de listes demandée - il me semble.

[lyceen95]

Perso, j'ai juste lu l'énoncé, et les différentes réponses, je n'ai pas cherché à résoudre réellement l'exercice. Mais après avoir lu tout ça, j'ai toujours du mal à bien visualiser la question.

Si j'étais élève, une des pistes que j'essaierais, pour me mettre en train, c'est de faire un dessin.
Pas sûr du tout que ce soit la meilleure piste, mais je constate que c'est aussi le réflexe de Tournesol.
La piste suggérée par GBZM ( rechercher un point ... avant re rechercher tous les points), c'estaussi forcément un bon conseil. Commencer par une chose simple, avant de s'attquer au problème total.

Dans un exercice de niveau lycée, on aurait 2 ou 3 questions intermédiaires, avant cette question finale. Ici, c'est à l'étudiant de deviner lui-même les questions intermédiaires.

[tournesol]

Je ne suis pas d'accord . Pour moi l'objectif simple n'apporte rien.Il faut resoudre graphiquement le pb global .
L'algorithme est alors évident .

[tournesol]

Je donne un algo matriciel:
déclaration A(k,n)matrice
déclaration B(k,n)matrice
déclaration de k listes Li
pour i de 1 à k
pour j de 1 à n
aij prend la valeur d(Qi,Pj)
j suivant
i suivant
Pour j de 1 à n
m prend la valeur min sur i des aij ( à implémenter éventuellement)
pour i de 1 à k
si aij=m alors bij prend la valeur 1
i suivant
j suivant
pour i de 1 à k
pour j de 1 à n
si bij=1 alors mettre Pj dans Li
j suivant
i suivant

[GaBuZoMeu]

C'est marrant, tournesol. Tu déclares "l'objectif simple n'apporte rien" mais dans l'algorithme que tu écris tu as bien l'étape

Pour j de 1 à n
m prend la valeur min sur i des aij ( à implémenter éventuellement)

qui est exactement l'objectif simple que je donnais.
Et c'est ce qui sert ensuite pour fabriquer la liste de listes de points demandée.

[tournesol]

L'objectif simple est une partie de l'algorithme mais je ne l'ai perçu pendant ma phase de recherche qu'après avoir fait un dessin .
J'ai dessiné des points P et des points Q .
Pour remplir la liste 1 , je me suis demandé si P1 était candidat . le point le plus proche etant Q3 , et non Q1 , P1 n'est pasdans L1 . Je peux déja mettre P1 dans la liste 3 , mais je dois passer par une matrice d'indicateurs car ce point peut ne pas être unique . Bref en dessinant j'ai tout compris , en particulier que ton objectif simple est une étape de l'algorithme .

[fatal_error]

hi

On peut simplifier un peu plus la formulation en prenant dans l'autre sens

La liste L_i correspond à Q_i.
On cherche les P pour qui le Q le plus proche est Q_i. Ils vont dans L_i.

il reste plus qu'à, comme l'a suggéré gbzm associer pour chaque P son Q_i (où L_i)

pour ma part je dessine pas, mais j'ai une visualisation mentale 2D, des liste L_i, comme un histogramme, avec en abscisse les Q_i régulièrement espacés et chaque P qui va se greffer dans une des listes

[GaBuZoMeu]

Petit bémol : il n'y a pas forcément un seul Q_p le plus proche d'un P_j donné ; il peut y en avoir plusieurs.