Inequations
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 30 Sep 2012, 14:45
par Fr4NgUs » 30 Sep 2012, 14:45

déterminer en fonction de a, le plus petit réel k(a) tel que:
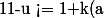u $)
.
pour tout u appartenant ]0;a]
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 30 Sep 2012, 14:56
par BertrandR » 30 Sep 2012, 14:56
Fr4NgUs a écrit:Soit a appartient ]0,1[ déterminer en fonction de a le plus petit réel k(a) tel que :
1/(1-u) inférieur ou égale 1+ k(a)u
De la même façon que dans votre autre post (intégrale généralisée), commencez par faire un effort de recherche avant de poster un message, qui en plus est dépourvu de toute question, ou interrogation destinée aux autres membres. Vous donnez seulement un énoncé comme si nous devions vous en donner la solution.
Déjà expliquer votre démarche et ce qui vous pose problème serait un bon début.
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 30 Sep 2012, 15:21
par Fr4NgUs » 30 Sep 2012, 15:21
BertrandR a écrit:De la même façon que dans votre autre post (intégrale généralisée), commencez par faire un effort de recherche avant de poster un message, qui en plus est dépourvu de toute question, ou interrogation destinée aux autres membres. Vous donnez seulement un énoncé comme si nous devions vous en donner la solution.
Déjà expliquer votre démarche et ce qui vous pose problème serait un bon début.
Bonjour, pour l'exercice précédent j'ai compris en regardant dans mon bouquin

cependant , la je crois sentir qu'il faut utiliser la bijection , mais je n'arrive pas à voir qu'elle fonction il faut faire intervenir , quelle fonction faut il étudier pour trouver ce réel. Après je vois pour la suite.
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 30 Sep 2012, 18:42
par Fr4NgUs » 30 Sep 2012, 18:42
Fr4NgUs a écrit:Bonjour, pour l'exercice précédent j'ai compris en regardant dans mon bouquin

cependant , la je crois sentir qu'il faut utiliser la bijection , mais je n'arrive pas à voir qu'elle fonction il faut faire intervenir , quelle fonction faut il étudier pour trouver ce réel. Après je vois pour la suite.
S'il vous plaît je n'ai toujours pas trouvé comment faire.
Serait-il possible au moins d'avoir une piste ?
Merci à vous.
-
BertrandR
- Membre Naturel
- Messages: 77
- Enregistré le: 25 Oct 2007, 15:13
-
 par BertrandR » 30 Sep 2012, 21:55
par BertrandR » 30 Sep 2012, 21:55
Fr4NgUs a écrit:S'il vous plaît je n'ai toujours pas trouvé comment faire.
Serait-il possible au moins d'avoir une piste ?
Merci à vous.
Indication :
Prouver que
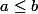
est équivalent à prouver que
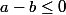
.
A méditer
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 30 Sep 2012, 22:05
par Fr4NgUs » 30 Sep 2012, 22:05
BertrandR a écrit:Indication :
Prouver que
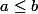
est équivalent à prouver que
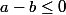
.
A méditer
D'accord , je vais méditer alors si la réflexion ne m'amène pas à la réponse.
Bonne idée !

-
Anonyme
 par Anonyme » 30 Sep 2012, 22:08
par Anonyme » 30 Sep 2012, 22:08
Fr4NgUs a écrit:
déterminer en fonction de a, le plus petit réel k(a) tel que:
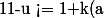u $)
.
Qu'est ce que représente

-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 30 Sep 2012, 22:09
par Fr4NgUs » 30 Sep 2012, 22:09
ptitnoir a écrit:Qu'est ce que représente

Je n'en ai pas la moindre idée

j'ai ajouté une infos dans l'énoncé j'avais oublié de préciser
-
Anonyme
 par Anonyme » 01 Oct 2012, 11:01
par Anonyme » 01 Oct 2012, 11:01
Il y a peut être une étude d'une famille de fonctions dans l'air ?
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 15:54
par Fr4NgUs » 01 Oct 2012, 15:54
ptitnoir a écrit:Il y a peut être une étude d'une famille de fonctions dans l'air ?
Je ne sais pas.
J'ai pensé à étudier la fonction k(a), mais je ne sais pas du tout ce que je fais j'obtiens :
k(a)=> 1/1-u et après je sais pas quoi faire de ça ?
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 16:00
par Fr4NgUs » 01 Oct 2012, 16:00
Fr4NgUs a écrit:Je ne sais pas.
J'ai pensé à étudier la fonction k(a), mais je ne sais pas du tout ce que je fais j'obtiens :
k(a)=> 1/1-u et après je sais pas quoi faire de ça ?
J'ai dérivé, démontré que k(a) strictement croissante et ensuite dressé le tableau de variation, et dois-je prendre le minimum pour avoir la réponse ?
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 18:44
par Fr4NgUs » 01 Oct 2012, 18:44
Personne n'a d'idées ? sinon j'abandonne tan pis :D
-
Stephanelam
- Membre Relatif
- Messages: 327
- Enregistré le: 11 Fév 2010, 17:43
-
 par Stephanelam » 01 Oct 2012, 19:10
par Stephanelam » 01 Oct 2012, 19:10
Fr4NgUs a écrit:
déterminer en fonction de a, le plus petit réel k(a) tel que:
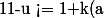u $)
.
pour tout u appartenant ]0;a]
On n'a pas assez d'informations pour traiter l'exo : qui est k ? dans quoi est défini a ?
Et puis c'est assez bizarre d'appeler un réel u, mais bon, passons.
:happy3:
Ah oui, pardon, a est dans ]0,1[. N'empêche qu'on ne sait toujours pas qui est k.
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 19:36
par Fr4NgUs » 01 Oct 2012, 19:36
Stephanelam a écrit:On n'a pas assez d'informations pour traiter l'exo : qui est k ? dans quoi est défini a ?
Et puis c'est assez bizarre d'appeler un réel u, mais bon, passons.
:happy3:
Tout est clairement précisé dans le premier post.
-
Stephanelam
- Membre Relatif
- Messages: 327
- Enregistré le: 11 Fév 2010, 17:43
-
 par Stephanelam » 01 Oct 2012, 19:56
par Stephanelam » 01 Oct 2012, 19:56
Fr4NgUs a écrit:Tout est clairement précisé dans le premier post.
J'ai édité, a est effectivement défini, mais pas k, donc sauf erreur de ma part, on ne sait pas ce que représente k(a).
-
Anonyme
 par Anonyme » 01 Oct 2012, 20:00
par Anonyme » 01 Oct 2012, 20:00
Voici le résultat que j'ai trouvé
= \fra{1}{1-a})
Merci à BertrandR de confirmer quelle est l'expression de la fonction k
@Stephanelam)
est un réel qui dépend du reel

donc on peut considérer que c'est une fonction réelle à variable réelle
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 20:05
par Fr4NgUs » 01 Oct 2012, 20:05
ptitnoir a écrit:Voici le résultat que j'ai trouvé
= \fra{a}{1-a})
Merci à BertrandR de confirmer quelle est l'expression de la fonction k
J'ai vraiment donné toutes les infos que j'avais.
Je ne peux être plus éxplicite
-
Stephanelam
- Membre Relatif
- Messages: 327
- Enregistré le: 11 Fév 2010, 17:43
-
 par Stephanelam » 01 Oct 2012, 20:09
par Stephanelam » 01 Oct 2012, 20:09
ptitnoir a écrit:@Stephanelam)
est un réel qui dépend du reel

donc on peut considérer que c'est une fonction réelle à variable réelle
Ah, ok, je ne savais pas qu'on pouvait sortir ça comme ça, en tout cas je n'ai jamais vu de cas où k n'est pas définie ... merci pour l'info.
:jap:
-
Fr4NgUs
- Membre Naturel
- Messages: 75
- Enregistré le: 29 Sep 2012, 17:38
-
 par Fr4NgUs » 01 Oct 2012, 20:09
par Fr4NgUs » 01 Oct 2012, 20:09
ptitnoir a écrit:Voici le résultat que j'ai trouvé
= \fra{a}{1-a})
Merci à BertrandR de confirmer quelle est l'expression de la fonction k
@Stephanelam)
est un réel qui dépend du reel

donc on peut considérer que c'est une fonction réelle à variable réelle
Comment en est-tu arrivé à ce résiltat ? Peux-tu expliquer ta démarche rapidement s'il te plaît ?
k je pense que c'est le nom de la fonction

-
Anonyme
 par Anonyme » 01 Oct 2012, 20:36
par Anonyme » 01 Oct 2012, 20:36
u)
donc
u )\le 0)
donc
+k(a)u)}{1-u} \le 0)
donc
+k(a)u \le 0)
donc
(1-u))
....etc....
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 58 invités
cependant , la je crois sentir qu'il faut utiliser la bijection , mais je n'arrive pas à voir qu'elle fonction il faut faire intervenir , quelle fonction faut il étudier pour trouver ce réel. Après je vois pour la suite.
.
est un réel qui dépend du reel
donc on peut considérer que c'est une fonction réelle à variable réelle