Bonjour, petit problème de maths où je suis perdu :
montrer que ln(1+x)<x pour tout x de -1 à +infini
Comment résoudre ca avec des x des deux cotés
Inéquations avec ln
4 messages
- Page 1 sur 1
Re: inéquations avec ln
a mon avis, tu ne prouveras rien avec des inégalités car elle elle partent de la comparaison à laquelle tu veux aboutir.
l'exercice est le même que
étudier le signe de ln(1+x)-x sur ]-1; +oo[
l'exercice est le même que
étudier le signe de ln(1+x)-x sur ]-1; +oo[
Modifié en dernier par pascal16 le 26 Aoû 2018, 17:48, modifié 1 fois.
Re: inéquations avec ln
Bonjour,
Tout d'abord, c'est faux : ?
?
Si tu as vu l'inégalité des accroissements finis, on peut l'utiliser en distinguant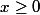 et
et 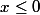 .
.
Par exemple, pour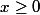 ,
,  \leq 1) , donc
, donc  - \ln(1+0) \leq 1(x-0)) .
.
Idem pour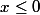 .
.
Tout d'abord, c'est faux :
Si tu as vu l'inégalité des accroissements finis, on peut l'utiliser en distinguant
Par exemple, pour
Idem pour
Re: inéquations avec ln
Salut,
Etudier les variations de f(x) = ln(1+x) - x sur ]-1 ; +oo[
f'(x) = ...
...
Tu devrais pouvoir alors montrer que f est maximum pour x = 0 et que ce max est f(0) = 0
Et puis conclure ...

Etudier les variations de f(x) = ln(1+x) - x sur ]-1 ; +oo[
f'(x) = ...
...
Tu devrais pouvoir alors montrer que f est maximum pour x = 0 et que ce max est f(0) = 0
Et puis conclure ...
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 18 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
