Inéquation

par **FLBP** » 03 Déc 2019, 20:55

Bonjour à tous, je bloque sur un problème, le voici :

Soit

une suite d'entiers positifs strictement croissante. Montrer qu'il existe un unique

tel que :

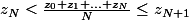
Merci par avance

par **tournesol** » 04 Déc 2019, 10:46

Soit une suite arithmetique de premier terme

et de raison r .
Soit

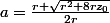
N doit vérifier : N<a et N

a .

par **tournesol** » 04 Déc 2019, 12:09

Je me suis compliqué la vie pour mon contre exemple : avec

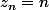
ça ne fonctionne pas .

par **FLBP** » 04 Déc 2019, 12:21

Merci, pour ta réponse.

par **GaBuZoMeu** » 04 Déc 2019, 14:13

Je comprends "positifs" comme "> 0". Le contre-exemple de Tournesol n'en est pas un si on prend les choses comme ça.

par **tournesol** » 04 Déc 2019, 14:56

Merci GaBuZoMeu
Mes contre exemples sont faux suite à des erreurs de calcul . Désolé .
Je vais chercher l'exo .

par **tournesol** » 04 Déc 2019, 18:30

La proposition est équivalente à

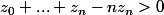
et

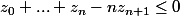
ie

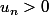
et

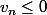
On a

.
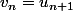
La proposition est donc équivalente à

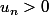
et

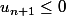
On a

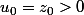
est une suite strictement décroissante d'entiers donc elle prend des valeurs négatives .
Soit i le plus petit entier tel que

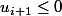
alors

.
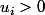
Il est alors immédiat que i est l'unique entier cherché .