Inégalites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 13:29
Ben314 a écrit:Pssssst,La dérivée, ça serait pas plutôt
\ =\ n(n-1)a^{n-1}-n(n-1)a^{n-2}b\ =\ n(n-1)(a-b)a^{n-2}\)
qui change de signe pour
?
(ce qui simplifie "légèrement" la suite :zen: )
Et pour le 1), perso., pour étudier le signe de
=\frac {1 + a^7}{1 + a} - \dfrac 1 4)
, j'aurais écrit que
=\frac {4(1 + a^7)-(1+a)}{4(1 + a)})
et j'aurai étudié le signe du numérateur (en le dérivant).
Ca doit à peu prés revenir au même mais avec des calculs sans doute un peu moins gros.
merci pour les remarques
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 13:46
Ben314 a écrit:Pssssst,La dérivée, ça serait pas plutôt
qui change de signe pour
?
(ce qui simplifie "légèrement" la suite :zen: )
Et pour le 1), perso., pour étudier le signe de
, j'aurais écrit que
et j'aurai étudié le signe du numérateur (en le dérivant).
Ca doit à peu prés revenir au même mais avec des calculs sans doute un peu moins gros.
certes oui ... mais ne pas oublier que 1 + a change de signe aussi ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 13:53
adamNIDO a écrit:Pour
Iposant
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {(1+a^7)'(1+a)-(1+a)'(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {(7 a^6)(1+a)-(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+7 a^7-1-a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+6 a^7-1)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
on peut poser encore une autre fonction par exemple :
=7 a^6+6 a^7-1)
de meme
=42a^5+42a^6=(42+a)a^6)
=-42)
si
alors
\geq 0)
si
alors
\leq 0)
donc
admet un minimum en
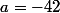
donc
=7(-42)^6+6(-42)^5-1=37639074815)
donc h est positive
ce qui amène que
l'est aussi
en conclusion
I 
est vraie
est ce que j'ai fait une bonne rédaction ?
attention pourquoi écrire h'(a) = -42 ? ....
h'(a) = 0 a = -42 ou a = 0
ensuite
.... donc g' > 0 mais on n'a pas encore le signe de g
g est croissante sur ]-oo, -1[ et sur ]-1, +oo[
et il faut déterminer son signe ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 14:25
zygomatique a écrit:attention pourquoi écrire h'(a) = -42 ? ....
h'(a) = 0 a = -42 ou a = 0
ensuite
si
alors
 \leq 0)
si
alors
 \geq 0)
donc h admet un minimum en point a=-42
.... donc g' > 0 mais on n'a pas encore le signe de g
g est croissante sur ]-oo, -1[ et sur ]-1, +oo[
et il faut déterminer son signe ....
h'(a) = 0 a = -42 ou a = 0
ensuite
si
alors
car
si
alors
car
donc h admet un minimum en point a=-42
=-1)
je suis coincé la
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 14:40
effectivement .... et l'étude des limites de h montre qu'elle change de signe ....
essaie la proposition de ben314 .... pour voir ....
trace cette fonction sur un grapheur .... pour voir ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 14:47
zygomatique a écrit:effectivement .... et l'étude des limites de h montre qu'elle change de signe ....
essaie la proposition de ben314 .... pour voir ....
trace cette fonction sur un grapheur .... pour voir ...
je pense que le but de l'exercice est d'utilise les tableaux de variations que je les maitrise pas du tout mais vraiment je veux les apprendres même que je suis un petit peu frustré a cause du stress et du manque de temps
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 14:51
 = 6a^7 + 7a^6 - 1 \\ h'(a) = 42a^5(a + 1))
tu as fait une erreur dans la dérivée !!!
h'(a) a même signe que a(a + 1) donc est positif à l'extérieur de [-1 0] et négatif dans [-1, 0]
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 15:49
zygomatique a écrit:tu as fait une erreur dans la dérivée !!!
h'(a) a même signe que a(a + 1) donc est positif à l'extérieur de [-1 0] et négatif dans [-1, 0]
oui monsieur vous êtes raison,
posant
donc
on peut poser encore une autre fonction par exemple :
de meme
=42a^5+42a^6=42a^5(a + 1))
=0 \Longleftrightarrow a=-1 \text{ou} a=0)
h'(a) a même signe que a(a + 1) donc est positif à l'extérieur de [-1 0] et négatif dans [-1, 0]
donc
admet un minimum en
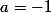
or
=0)
et
=-\infty)
and
=+\infty)
donc admet un minimum -1 et maximum 0
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 15:55
tu as donc le signe de h
h s'annule entre 0 et 1 (TVI car h(0) = -1 et h(1) = 12)
donc il existe u tel que h(u) = 0
si x < u alors h donc g' < 0 et si x> u alors h donc g' > 0
.... tu peux faire le tableau de variation de g donc .... et déterminer son signe ..
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 16:03
 = a^6 - a^5 + a^4 - a^3+ a^2 - a + \dfrac 3 4 = a(a - 1)(1 + a^2 + a^4) + \dfrac 3 4)
a a - 1 0
a > 1 => a - 1 > 0 donc g(a) > 0
il ne te reste plus que le cas 0 < a < 1 :ptdr:
PS : et on comprend d'où sort le 3/4 .... :lol3:
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 15 Nov 2014, 16:15
Perso, j'ai pas trop compris le 3/4 : avec 1/2 à la place, c'est toujours vrai (et c'est même "plus fort" avec une constante légèrement plus simple) et ça le serait même avec 3/8 voire 23/63...
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 17:29
zygomatique a écrit:tu as donc le signe de h
h s'annule entre 0 et 1 (TVI car h(0) = -1 et h(1) = 12)
donc il existe u tel que h(u) = 0
si x u alors h donc g' > 0
.... tu peux faire le tableau de variation de g donc .... et déterminer son signe ..
je pense qu'on doit prendre
et pas
donc comme
=-1,h(-1)=0[)
et h(0)=-1 alors il existe
tel que
 = 0)
??
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 17:32
un peu de sérieux ::
y a-t-il 0 entre -1 et 0 ?
y a-t-il 0 entre h(0) = -1 et h(1) = 12 ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 17:54
zygomatique a écrit:un peu de sérieux ::
y a-t-il 0 entre -1 et 0 ?
y a-t-il 0 entre h(0) = -1 et h(1) = 12 ....
mais pourquoi monsieur vous avez choisie h(1)=12 et pas autre valeur
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 19:43
adamNIDO a écrit:mais pourquoi monsieur vous avez choisie h(1)=12 et pas autre valeur
ben si une fonction continue varie de -1 (en 0) à 12 (en 1) alors elle passe par 0 (au moins une fois)
...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 19:44
bonsoir monsieur zygomatique
j'ai une autre question
si j'ai
et
)
merci pour votre attention
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 19:45
je t'ai quand même résolu une bonne partie de pb à 16h03 ...
de façon beaucoup plus simple ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 19:45
zygomatique a écrit:ben si une fonction continue varie de -1 (en 0) à 12 (en 1) alors elle passe par 0 (au moins une fois)
...
effectivement oui mais moi jetais concentre sur la notion de maximum et minimum c'est parce que j'ai pris que 0 et -1 donc pas 12
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
par adamNIDO » 15 Nov 2014, 19:49
zygomatique a écrit:je t'ai quand même résolu une bonne partie de pb à 16h03 ...
de façon beaucoup plus simple ....
oui mais je veux continue par La première méthode pour rafraîchir et entretenir les notions de tableau de variation et T.V.I
merci beaucoup pour votre temps
-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
par zygomatique » 15 Nov 2014, 19:51
adamNIDO a écrit:bonsoir monsieur zygomatique
j'ai une autre question
si j'ai
et
merci pour votre attention
prend x = -0.1 et y = 1
prend x = 10 et y = 0.001
prend x = 100 et y = -1
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 24 invités
