Inégalites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 08:55
par adamNIDO » 15 Nov 2014, 08:55

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 09:28
par zygomatique » 15 Nov 2014, 09:28
salut
la première est fausse pour a = 1 ....
pour la deuxième étudie la fonction
 = (n - 1)a^n + b^n - na^{n - 1}b)
pour b fixé ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 09:30
par adamNIDO » 15 Nov 2014, 09:30
zygomatique a écrit:salut
la première est fausse pour a = 1 ....
donc sera

au lieu de


-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 09:36
par zygomatique » 15 Nov 2014, 09:36
^2 \ge 0 a^2 + b^2 \ge 2ab \\ (b - c)^2 \ge 0 b^2 + c^2 \ge 2bc \\ (c - a)^2 \ge 0 c^2 + a^2 \ge 2ac)
et il suffit d'ajouter membre à membre ...
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 09:48
par adamNIDO » 15 Nov 2014, 09:48
zygomatique a écrit:^2 \ge 0 a^2 + b^2 \ge 2ab \\ (b - c)^2 \ge 0 b^2 + c^2 \ge 2bc \\ (c - a)^2 \ge 0 c^2 + a^2 \ge 2ac)
et il suffit d'ajouter membre à membre ...
merci beaucoup mais pour quelle inégalité

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 10:10
par zygomatique » 15 Nov 2014, 10:10
adamNIDO a écrit:merci beaucoup mais pour quelle inégalité
un peu de sérieux ... car tu me montres que tu n'as pas fait ce qu'il est suffisant de faire ....

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 10:13
par adamNIDO » 15 Nov 2014, 10:13
zygomatique a écrit:un peu de sérieux ... car tu me montres que tu n'as pas fait ce qu'il est suffisant de faire ....

non je suis entrain de faire les exercices

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 10:22
par zygomatique » 15 Nov 2014, 10:22
c'est vrai pour a = -1
pour

::

il suffit d'étudier cette fonction
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 10:24
par adamNIDO » 15 Nov 2014, 10:24
zygomatique a écrit:salut
la première est fausse pour a = 1 ....
pour la deuxième étudie la fonction
 = (n - 1)a^n + b^n - na^{n - 1}b)
pour b fixé ....
pour
II a^n+b^n\geq na^{n-1}b)
on étudie la fonction la fonction
 = (n - 1)a^n + b^n - na^{n - 1}b)
pour b fixé ....[/quote]
=(n(n-1)a-b)a^{n-2} \\<br /><br />f'(a)=0 \Longleftrightarrow a=\dfrac{b}{n(n-1)})
si
} \Longrightarrow f'(a)\geq 0)
si
} \Longrightarrow f'(a)\leq 0)
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 10:46
par adamNIDO » 15 Nov 2014, 10:46
zygomatique a écrit:c'est vrai pour a = -1
pour

::

il suffit d'étudier cette fonction
posant
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
donc
=\dfrac {7a^6-6a^7-1}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 11:09
par zygomatique » 15 Nov 2014, 11:09
adamNIDO a écrit:pour
II a^n+b^n\geq na^{n-1}b)
on étudie la fonction la fonction
 = (n - 1)a^n + b^n - na^{n - 1}b)
pour b fixé ....
=(n(n-1)a-b)a^{n-2} \\<br /><br />f'(a)=0 \Longleftrightarrow a=\dfrac{b}{n(n-1)})
si
} \Longrightarrow f'(a)\geq 0)
si
} \Longrightarrow f'(a)\leq 0)
donc f admet un minimum en a = ....
or f(a) = ...
donc ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 11:11
par zygomatique » 15 Nov 2014, 11:11
adamNIDO a écrit:posant
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
donc
=\dfrac {7a^6-6a^7-1}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
es-tu sur du numérateur ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 11:20
par adamNIDO » 15 Nov 2014, 11:20
=(n(n-1)a-b)a^{n-2} \\<br /><br />f'(a)=0 \Longleftrightarrow a=\dfrac{b}{n(n-1)})
si
} \Longrightarrow f'(a)\geq 0)
si
} \Longrightarrow f'(a)\leq 0)
donc f admet un minimum en
})
or
 =[\dfrac{(n-1)}{n^n(n-1)^n}+1]b^n\geq 0)
car

donc f est positive pour tout

desolé si je suis un peu lent car j'ai oublié beaucoup de notion en maths
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 11:24
par adamNIDO » 15 Nov 2014, 11:24
zygomatique a écrit:es-tu sur du numérateur ?
posant
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
donc
=\dfrac {(1+a^7)'(1+a)-(1+a)'(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {(7 a^6)(1+a)-(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+7 a^7-1-a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+6 a^7-1)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
on peut poser encore une autre fonction par exemple :
=7 a^6+6 a^7-1)
de meme
=42a^5+42a^6=(42+a)a^6)
=-42)
si

alors
\geq 0)
si

alors
\leq 0)
donc

admet un minimum en
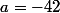
donc
=7(-42)^6+6(-42)^5-1=37639074815)

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 12:03
par zygomatique » 15 Nov 2014, 12:03
adamNIDO a écrit:=(n(n-1)a-b)a^{n-2} \\<br /><br />f'(a)=0 \Longleftrightarrow a=\dfrac{b}{n(n-1)})
si
} \Longrightarrow f'(a)\geq 0)
si
} \Longrightarrow f'(a)\leq 0)
donc f admet un minimum en
})
or
 =[\dfrac{(n-1)}{n^n(n-1)^n}+1]b^n\geq 0)
car

donc f est positive pour tout

desolé si je suis un peu lent car j'ai oublié beaucoup de notion en maths
conclusion ?
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 12:08
par adamNIDO » 15 Nov 2014, 12:08
zygomatique a écrit:conclusion ?
pour la conclusion on peut dire que :II[/B]
a^n+b^n\geq na^{n-1}b)
est vraie

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 12:15
par zygomatique » 15 Nov 2014, 12:15
la première ligne de g'(a) est inutile ...
posons
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
donc
=\dfrac {(7 a^6)(1+a)-(1+a^7)}{(1 + a)^2} = \dfrac {7 a^6+7 a^7-1-a^7}{(1 + a)^2} =\dfrac {7 a^6+6 a^7-1}{(1 + a)^2})
suffit amplement ....
et l'étude du signe alors ?
étudie la fonction
 = 6a^7 + 7a^6 - 1)
pour étudier le signe du numérateur de g' ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 12:20
par adamNIDO » 15 Nov 2014, 12:20
zygomatique a écrit:la première ligne de g'(a) est inutile ...
posons
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
donc
=\dfrac {(7 a^6)(1+a)-(1+a^7)}{(1 + a)^2} = \dfrac {7 a^6+7 a^7-1-a^7}{(1 + a)^2} =\dfrac {7 a^6+6 a^7-1}{(1 + a)^2})
suffit amplement ....
et l'étude du signe alors ?
étudie la fonction
 = 6a^7 + 7a^6 - 1)
pour étudier le signe du numérateur de g' ....
oui j'ai fait ca veuillez monsieur verifier ce que j'ai fait
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 12:33
par adamNIDO » 15 Nov 2014, 12:33
Pour
Iposant
=\dfrac {1 + a^7}{1 + a} - \dfrac 1 4 \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {(1+a^7)'(1+a)-(1+a)'(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {(7 a^6)(1+a)-(1+a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+7 a^7-1-a^7)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
=\dfrac {7 a^6+6 a^7-1)}{(1 + a)^2} \quad \forall a\in \mathbb{R} \backslash \{-1})
on peut poser encore une autre fonction par exemple :
=7 a^6+6 a^7-1)
de meme
=42a^5+42a^6=(42+a)a^6)
=0 \Longleftrightarrow a=-42)
ou

si

alors
\geq 0)
si

alors
\leq 0)
donc

admet un minimum en
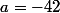
donc
=7(-42)^6+6(-42)^5-1=37639074815)
donc h est positive

ce qui amène que

l'est aussi
en conclusion
I 
est vraie
est ce que j'ai fait une bonne rédaction ?

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Nov 2014, 13:10
par Ben314 » 15 Nov 2014, 13:10
Pssssst,
adamNIDO a écrit: = (n - 1)a^n + b^n - na^{n - 1}b)
=(n(n-1)a-b)a^{n-2})
La dérivée, ça serait pas plutôt
\ =\ n(n-1)a^{n-1}-n(n-1)a^{n-2}b\ =\ n(n-1)(a-b)a^{n-2}\)
qui change de signe pour

?
(ce qui simplifie "légèrement" la suite :zen: )
Et pour le 1), perso., pour étudier le signe de
=\frac {1 + a^7}{1 + a} - \dfrac 1 4)
, j'aurais écrit que
=\frac {4(1 + a^7)-(1+a)}{4(1 + a)})
et j'aurai étudié le signe du numérateur (en le dérivant).
Ca doit à peu prés revenir au même mais avec des calculs sans doute un peu moins gros.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 26 invités
 = (n - 1)a^n + b^n - na^{n - 1}b)