Inégalites
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 15 Nov 2014, 20:06
par Ben314 » 15 Nov 2014, 20:06
adamNIDO a écrit:si j'ai

et
)
C'est dans quelle classe qu'on voit qu'un inégalité, si on multiplie les deux terms par un nombre négatif, elle "change de sens" ?
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 20:10
par adamNIDO » 15 Nov 2014, 20:10
zygomatique a écrit:prend x = -0.1 et y = 1
prend x = 10 et y = 0.001
prend x = 100 et y = -1
....
donc vous m'avez donné des contre-exemples donc je vais vous dire si

et

alors on a

j'ai pense a ca pour puisse écrire:
quand
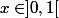
si

(car x(x-1) admet un minimum en point
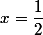
) donc
(x^4+x^2+1)>- \dfrac{3}{4})
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 20:17
par adamNIDO » 15 Nov 2014, 20:17
Ben314 a écrit:C'est dans quelle classe qu'on voit qu'un inégalité, si on multiplie les deux terms par un nombre négatif, elle "change de sens" ?
je pense que si vous avez le produit d'un terme positif et un terme négatif, il est supérieur au maximum de l'un positif multiplié pour le minimum de la négative.

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 15 Nov 2014, 20:36
par zygomatique » 15 Nov 2014, 20:36
plus précisément on a ::
0 < x < a
b < y < 0 <=> 0 < -y < -b
donc
0 < -xy < -ab <=> ab < xy < 0
....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 15 Nov 2014, 21:39
par adamNIDO » 15 Nov 2014, 21:39
[quote="zygomatique"]plus précisément on a ::
0 0 ab -\dfrac{1}{4}[/TEX](car x(x-1) admet un minimum en point
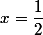
) donc
(x^4+x^2+1)>- \dfrac{3}{4})
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 16 Nov 2014, 18:48
par adamNIDO » 16 Nov 2014, 18:48
Bonsoir
Pouvez-vous m'aider à résoudre ce exercices
merci

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Nov 2014, 19:33
par zygomatique » 16 Nov 2014, 19:33
lequel ? ...........
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 16 Nov 2014, 20:11
par adamNIDO » 16 Nov 2014, 20:11
zygomatique a écrit:lequel ? ...........
bonsoir monsieur
je pense qu'on a terminé I il nous reste que V et VI car IV déjà fait par moi

-
zygomatique
- Habitué(e)
- Messages: 6928
- Enregistré le: 20 Mar 2014, 12:31
-
 par zygomatique » 16 Nov 2014, 21:55
par zygomatique » 16 Nov 2014, 21:55
adamNIDO a écrit:bonsoir monsieur
je pense qu'on a terminé I il nous reste que V et VI car IV déjà fait par moi
pour l'instant je ne vois rien d'intéressant ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2014, 23:37
par Ben314 » 16 Nov 2014, 23:37
Pour la
V, calcule
^2+(b^2-c^2)^2+(c^2-a^2)^2)
Pour la
VI, calcule
^2+(\frac{b}{c}-\frac{c}{a})^2+(\frac{c}{a}-\frac{a}{b})^2)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 16 Nov 2014, 23:44
par Ben314 » 16 Nov 2014, 23:44
Pour la
V,
^2+b^2(c-a)^2+c^2(a-b)^2\ \geq\ 0)
ainsi que
^2+(b^2-c^2)^2+(c^2-a^2)^2\ \geq\ 0)
Pour la
VI,
^2+(\frac{b}{c}-\frac{c}{a})^2+(\frac{c}{a}-\frac{a}{b})^2\ \geq\ 0)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
adamNIDO
- Membre Rationnel
- Messages: 967
- Enregistré le: 22 Jan 2014, 00:47
-
 par adamNIDO » 17 Nov 2014, 11:34
par adamNIDO » 17 Nov 2014, 11:34
Ben314 a écrit:Pour la
V,
^2+b^2(c-a)^2+c^2(a-b)^2\ \geq\ 0)
ainsi que
^2+(b^2-c^2)^2+(c^2-a^2)^2\ \geq\ 0)
Pour la
VI,
^2+(\frac{b}{c}-\frac{c}{a})^2+(\frac{c}{a}-\frac{a}{b})^2\ \geq\ 0)
oui ca marche bien
un grand merci pour votre temps
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
et
