Inégalités
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Avr 2012, 07:46
par Dinozzo13 » 04 Avr 2012, 07:46
Bonjour, je bloque encore sur un exercice portant sur les inégalités :
On donne

tels que
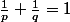
.
On me demande de démontrer que,

:

.
Je serais tenter d'étudier les variations de la fonction
= \frac{x^p}{p}-yx+ \frac{x^q}{q})
, mais je pense qu'il y a plus simple.
Merci d'avance pour votre aide/vos conseils :++:
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 04 Avr 2012, 08:22
par ev85 » 04 Avr 2012, 08:22
Dinozzo13 a écrit:Bonjour, je bloque encore sur un exercice portant sur les inégalités :
On donne

tels que
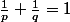
.
On me demande de démontrer que,

:

.
Je serais tenter d'étudier les variations de la fonction
= \frac{x^p}{p}-yx+ \frac{x^q}{q})
, mais je pense qu'il y a plus simple.
Merci d'avance pour votre aide/vos conseils :++:
Bonjour Dino.
Tu peux partir de

et utiliser la convexité de l'exponentielle.
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 04 Avr 2012, 11:24
par Dinozzo13 » 04 Avr 2012, 11:24
l'exponentielle est convexe donc :

.
Mais comment utiliser cette inégalité à partir de l'égalité que tu m'as moontrée ?
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 04 Avr 2012, 11:50
par gdlrdc » 04 Avr 2012, 11:50
la convexité te dit que f(tx+(1-t)y) est inférieur à tf(x) +(1-t)f(y) pour t entre 0 et 1, et pas seulement le cas particulier que tu as écrit.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Avr 2012, 11:50
par chan79 » 04 Avr 2012, 11:50
Dinozzo13 a écrit:Bonjour, je bloque encore sur un exercice portant sur les inégalités :
On donne

tels que
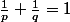
.
On me demande de démontrer que,

:

.
Salut
Vérifie le texte
avec p=q=x=2 et y=3, ça donne 6<=4
-
gdlrdc
- Membre Relatif
- Messages: 160
- Enregistré le: 24 Jan 2009, 18:11
-
 par gdlrdc » 04 Avr 2012, 11:55
par gdlrdc » 04 Avr 2012, 11:55
Ah bon !!!!? je dirais plutot 6 <= 6,5 ce qui est vrai.
oups, c'est vrai il a écrit x^q au lieu de y^q.
-
bend
- Membre Relatif
- Messages: 102
- Enregistré le: 10 Nov 2009, 16:02
-
 par bend » 04 Avr 2012, 12:07
par bend » 04 Avr 2012, 12:07
Dinozzo13 a écrit:l'exponentielle est convexe donc :

.
Mais comment utiliser cette inégalité à partir de l'égalité que tu m'as moontrée ?
Bonjour ,
comme il a dit ev85, tu peux utiliser
 = \frac{ln (x^{p})}{p} +\frac{ln (y^{q})}{q})
, et comme

est convexe et
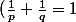)
,tu peux utiliser dans ce cas l'Inégalité de Jensen
Rappel ,:si

une fonction convexe et
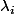
des reels tel que

et les
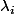
sont dans l'intervale [0,1] ,
alors
 \leq \Large \sum_{p=0}^{p=n}{\lambda_{i}} f(x_{i}))
Cordialement
-
Dinozzo13
- Membre Transcendant
- Messages: 3756
- Enregistré le: 21 Juin 2009, 21:54
-
 par Dinozzo13 » 05 Avr 2012, 22:18
par Dinozzo13 » 05 Avr 2012, 22:18
Salut !
Tout d'abord, merci pour l'aide apportée :++:
J'aurai une autre question :
Je dois démontrer que :

.
Je pose

et je montre que
)
est strict. décrois. à partir de
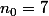
.
Ma question, serait de savoir s'il existe d'autres manières de résoudre cette question, merci d'avance :+++:
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 06 Avr 2012, 08:43
par ev85 » 06 Avr 2012, 08:43
Dinozzo13 a écrit:Salut !
Tout d'abord, merci pour l'aide apportée :++:
J'aurai une autre question :
Je dois démontrer que :

.
Je pose

et je montre que
)
est strict. décrois. à partir de
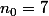
.
Ma question, serait de savoir s'il existe d'autres manières de résoudre cette question, merci d'avance :+++:
Bonjour Dino.
Tu peux remarquer que 7 est la partie entière de
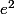
et étudier les variations de

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
tels que
.
:
.
, mais je pense qu'il y a plus simple.
.
.
et je montre que
est strict. décrois. à partir de
.