Hello,
cette question est très intéressante, et il existe d'autres exemples de telles fonctions, dans des cadres variés. En assistant aux oraux d'agreg cette année, j'ai cru voir deux résultats de ce type, mais ils n'étaient pas énoncés sous cette forme, mais plutôt utilisés pour d'autre résultats. Le premier concernait des séries de Fourier de fonctions à support compact (théorème de Shannon), l'autre concernait la preuve qu'un sev fermé de Lp inclus dans dans Linfini est de dimension finie.
Plus concrètement, pour un autre exemple de normes équivalentes sur un sous-espace vectoriel de fonctions de dimension infinie, tu peux regarder le problème 9 de "Problèmes-clefs de mathématiques supérieures" de GIANELLA, KRUST, TAIEB et TOSEL. Ils explicitent un exemple, un peu plus faible,d'espace vectoriel engendré par des séries trigonométriques lacunaires, sur lequel toutes les normes Lp, pour p entre 1 et 2, sont équivalentes. Ils énoncent en fait, mais sans démonstration, que toutes les normes Lp (1

p<

) sont équivalentes. Pour plus de renseignements, ils disent de se reporter au chapitre 5 du livre de Y. Katznelson, "An Introduction to Harmonic Analysis".
Luc
AlexisD a écrit:Bonjour à tous,
Je suis en train de lire une chose intéressant sur les suites de Rademacher dans le Queffélec-Zuily : Eléments d'analyse.
Dans l'espace probabilisé (

= [0,1], A, P), on considère donc le sous espace engendré par les variables de Rademacher
)
valant +1 et -1 avec probabilité 1/2.
Alors dans ce sous-espace, les normes Lp sont équivalentes. Ce sont les inégalités de Khintchine:
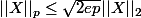
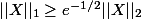
Je me demandais s'il existait d'autres espaces mesurés (par forcément probabilisés) dans lesquels on avait encore l'équivalence des nomes Lp.
Merci à celui ou à celle qui saura satisfaire ma curiosité.
