Inégalité d'Young
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
COTLOD
- Membre Relatif
- Messages: 104
- Enregistré le: 14 Sep 2008, 10:07
-
par COTLOD » 17 Fév 2009, 10:49
Bonjours,
J'ai commencé un exercice dans "calcul infinitésimal" dont je n'ai pas de solution. Il s'agit d'utiliser l'inégalité d'Young pour prouver une autre inégalité.
Inégalité (1) d'Young :
dt+\int_0^y g(u)du$$)
Inégalité (2) à démontrer :
+e^{y-1}$$)
La difficulté (je trouve) c'est que les conditions d'application de l'inégalité d'Young sont
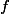
continue et strictement croissante sur
avec
=0$)
,
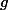
est sa réciproque sur
]$)
,
et
$)
or l'inégalité (2) est à démontrer pour tous
.
Merci d'avance pour vos idées.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 17 Fév 2009, 11:10
 dx + \int_0^b (e^x -1) dx)
Puis x -> x-1 et y-> y-1
-
COTLOD
- Membre Relatif
- Messages: 104
- Enregistré le: 14 Sep 2008, 10:07
-
par COTLOD » 17 Fév 2009, 11:54
Tu propose bien des changements de variables x->x-1 et y->y-1 pour les intégrales ? Si je ne me trompe pas on a :
dx=\int_1^{a+1} log(x)dx=[xlog(x)-x]_1^{a+1}=(a+1)log(a+1)-a$)
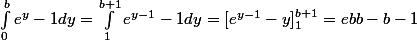
Je ne vois pas comment réduire.
-
ThSQ
- Membre Complexe
- Messages: 2077
- Enregistré le: 10 Oct 2007, 17:40
-
par ThSQ » 17 Fév 2009, 12:48
En fait, j'ai d'abord intégré la première inégalité puis remplacer mais on peut tout faire d'un coup comme toi. Tu es presque au bout là, tu peux factoriser (a+1)(b+1) "à gauche".
-
COTLOD
- Membre Relatif
- Messages: 104
- Enregistré le: 14 Sep 2008, 10:07
-
par COTLOD » 17 Fév 2009, 13:10
Merci pour cette solution mais elle me pose un problème : soit l'ingalité
+e^{y-1}$)
n'est démontrée que pour x>1 ; soit l'inégalité d'Young n'est pas utilisé dans les conditions que j'ai données (...
).
En effet, en reprenant les notations du calcul précédent, on établit
(b+1)\leq (a+1)log(a+1)+e^b$$)
avec a>0 (à cause de l'inégalité d'Young utilisée).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
