Inégalité
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Aoû 2009, 13:50
par ToToR_2000 » 13 Aoû 2009, 13:50
Bonjour à tous,
J'ai besoin de montrer l'inégalité suivante:
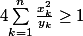
avec
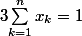
et
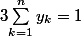
avec tous les
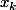
,
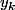
strictement positifs, l'égalité étant vraie si et seulement si

.
J'ai pensé à Cauchy-Schwartz, la convexité mais je ne vois pas trop comment s'en servir efficacement.
Si quelqu'un a des idées, je suis preneur.
Merci d'avance !
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Aoû 2009, 14:05
par ToToR_2000 » 13 Aoû 2009, 14:05
Je retire: c'est trivial avec Jensen + fonction inverse

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 13 Aoû 2009, 14:11
par Ericovitchi » 13 Aoû 2009, 14:11
Heu j'étais en train de chercher. Tu dis que c'est trivial ?
Jensen c'est
 \, \mathrm dx \right) \leq \int_0^1 f \circ \phi \left( x \right) \, \mathrm dx)
?
Tu prends quoi exactement comme fonctions ?
ou alors tu pars de
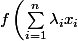 \leq \sum_{i=1}^n \lambda_i f \left( x_i \right))
?
-
ToToR_2000
- Membre Relatif
- Messages: 121
- Enregistré le: 26 Juin 2009, 17:33
-
 par ToToR_2000 » 13 Aoû 2009, 14:19
par ToToR_2000 » 13 Aoû 2009, 14:19
oui, je prends la forme discrète de Jensen sur
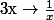
:
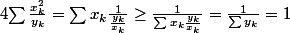

-
Ericovitchi
- Habitué(e)
- Messages: 7853
- Enregistré le: 18 Avr 2009, 13:24
-
 par Ericovitchi » 13 Aoû 2009, 14:35
par Ericovitchi » 13 Aoû 2009, 14:35
Ha oui OK. Bien joué. Pas si trivial que ça :doute2:
merci
-
Zweig
- Membre Complexe
- Messages: 2012
- Enregistré le: 02 Mar 2008, 02:52
-
 par Zweig » 14 Aoû 2009, 21:23
par Zweig » 14 Aoû 2009, 21:23
Avec Cauchy-Schwarz c'est direct :
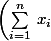^2 = \left(\sum^n_{i=1}\,\frac{x_i}{\sqrt{y_i}}\cdot \sqrt{y_i}\right)^2 \leq \left(\sum^n_{i=1}\,y_i\right)\left(\sum^n_{i=1} \,\frac{x^2_i}{y_i} \right))
D'où
^2}{\sum^n_{i=1}\,y_i} = 1)
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités