sachant que j'ai déja démontré le resultat suivant :
Inégalité partie entiére
5 messages
- Page 1 sur 1
Re: inégalité partie entiére
Salut,
C'est assez couillon comme truc : si tu écrit que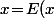\!+\!a) et
et 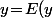\!+\!b) , ce que tu doit montrer, c'est que
, ce que tu doit montrer, c'est que
+E(y)+\Big(E(x)\!+\!E(y)\, {\blue [+1\text{ si }a\!+\!b\!\geq\!1]}\Big)\leq\Big(2E(x)\, {\blue [+1\text{ si }a\!\geq\!\frac12]}\Big)+\Big(2E(y)\ {\blue [+1\text{ si }b\!\geq\!\frac12]}\Big))
Et c'est évident vu que)
C'est assez couillon comme truc : si tu écrit que
Et c'est évident vu que
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: inégalité partie entiére
donc si j'ai bien compris il suffit de traiter les 4 cas possible ?(  et
et  ;
;  et
et  ;
;  et
et  ;
;  et
et  )
)
Re: inégalité partie entiére
mehdibj a écrit:donc si j'ai bien compris il suffit de traiter les 4 cas possible ?(et
;
et
;
et
;
et
)
Bonjour,
En fait il n'y a que 2 cas (solution de Ben314 dite autrement) :
1er cas) E(x+y)=E(x)+E(y)+1. Cela veut dire que l'un des 2 au moins (x ou y) a une partie décimale >=1/2, par exemple x.
Alors E(2x)>=2*E(x)+1, E(2y)>=2*E(y) (ceci est toujours vrai quelque soit y), et on aboutit à l'inégalité cherchée.
2ème cas) E(x+y)=E(x)+E(y). Avec E(2x)>=2*E(x) et E(2y)>=2*E(y), on aboutit aussi à l'inégalité cherchée.
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
