Inégalité de norme dans un evn
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MoonX
- Membre Naturel
- Messages: 85
- Enregistré le: 30 Oct 2016, 22:39
-
 par MoonX » 05 Nov 2017, 15:49
par MoonX » 05 Nov 2017, 15:49
Bonjour,
Soient
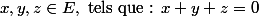
Je cherche à établir l'inégalité suivante :
)
Je ne sais pas trop comment démarrer. J'ai essayé d'utiliser l'hypothèse pour démarrer, mais je n'ai rien trouvé de concluant (je suis sûrement passé à coté de quelque chose)
-
LB2
- Habitué(e)
- Messages: 1504
- Enregistré le: 05 Nov 2017, 16:32
-
 par LB2 » 05 Nov 2017, 16:59
par LB2 » 05 Nov 2017, 16:59
Bonjour MoonX,
quelle inégalité connais tu pour une norme dans un evn ?
-
MoonX
- Membre Naturel
- Messages: 85
- Enregistré le: 30 Oct 2016, 22:39
-
 par MoonX » 05 Nov 2017, 17:13
par MoonX » 05 Nov 2017, 17:13
L'inégalité triangulaire seulement (et sa forme |N(x) - N(y) |<= N(x-y) )
J'ai essayé d'utiliser cette forme, mais je n'ai rien trouvé non plus

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 05 Nov 2017, 17:20
par Ben314 » 05 Nov 2017, 17:20
Salut,
Indication : Si
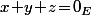
alors
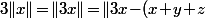\right\|\!=\!\left\|2x\!-\!y\!-\!z\right\|\!=\!\left\|(x\!-\!y)\!-\!(z\!-\!x)\right\|\cdots)
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
MoonX
- Membre Naturel
- Messages: 85
- Enregistré le: 30 Oct 2016, 22:39
-
 par MoonX » 05 Nov 2017, 17:44
par MoonX » 05 Nov 2017, 17:44
D'accord, ça marche très bien comme cela ! Je vois mieux :
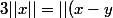 - (z-x)|| \leqslant ||x-y||+|| z-x||)
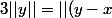 - (z-y)|| \leqslant ||y-x||+||z-y||)
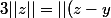 - (x-z)|| \leqslant ||z-y||+||z-x||)
D'où le résultat par somme de ces trois lignes !
Merci beaucoup pour votre aide.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités