Inégalité et module
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 16:16
par jonses » 02 Fév 2014, 16:16
Bonjour,
J'essaye de faire un exercice, mais ça fait déjà un bout de temps que je suis dessus (je suis presque sur le point de m'arracher les cheveux!) :
Soit
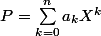
un polynôme de degré supérieur ou égal à 1 à coefficients complexes.
Je dois montrer que :
\, \mid \, \ge \mid\, \frac{a_n z^n}{2}\,\mid \big))
Si quelqu'un peut m'aider svp
Je vous remercie d'avance pour vos réponses
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Fév 2014, 16:33
par Doraki » 02 Fév 2014, 16:33
Ben commence sur un exemple.
Prend un polynôme au hasard, comme P(z) = 2z^3 + 3z + 5i.
Puis prend un réel positif au hasard, comme par exemple r = 1 milliard.
Peux-tu prouver que si |z| > 1 milliard, |P(z)| >= |z|^3 ?
Là c'est certainement un truc vrai, t'as juste à appliquer l'inégalité |z| > 1 milliard au bons endroits et dans le bons sens, même n'importe comment tu devrais largement pouvoir montrer l'inégalité.
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 16:40
par Rha » 02 Fév 2014, 16:40
Bonjour,
Si
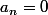
c'est immédiat.
Sinon, pour
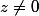
, en utilisant la définition de la valeur absolue de réels:
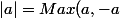)
, on a:
|}{|\frac{a_nz^n}{2}|} \geq 2\frac{a_n}{a_n} + \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n})
.
et
|}{|\frac{a_nz^n}{2}|} \geq - 2\frac{a_n}{a_n} - \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n})
.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 16:44
par jonses » 02 Fév 2014, 16:44
Doraki a écrit:Ben commence sur un exemple.
Prend un polynôme au hasard, comme P(z) = 2z^3 + 3z + 5i.
Puis prend un réel positif au hasard, comme par exemple r = 1 milliard.
Peux-tu prouver que si |z| > 1 milliard, |P(z)| >= |z|^3 ?
Là c'est certainement un truc vrai, t'as juste à appliquer l'inégalité |z| > 1 milliard au bons endroits et dans le bons sens, même n'importe comment tu devrais largement pouvoir montrer l'inégalité.
Justement, c'est parce que j'y arrive pas sur un exemple que je m'arrache les cheveux :mur:
Rha a écrit:Si
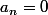
c'est immédiat.
Sinon, pour
, en utilisant la définition de la valeur absolue de réels:
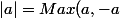)
, on a:
|}{|\frac{a_nz^n}{2}|} \geq 2\frac{a_n}{a_n} + \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n})
.
et
|}{|\frac{a_nz^n}{2}|} \geq - 2\frac{a_n}{a_n} - \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n})
.
Sauf que là c'est pas des réels, mais des complexes, je peux pas utilisé la définition de valeur absolue
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 16:53
par Rha » 02 Fév 2014, 16:53
Oula pardon!
Tu peux quand-même écrire pour

non nul:
|}{|\frac{a_nz^n}{2}|} = |\frac{P(z)}{\frac{a_nz^n}{2}}| = |2 + \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n}|)
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 16:56
par jonses » 02 Fév 2014, 16:56
Rha a écrit:Oula pardon!
Tu peux quand-même écrire pour

non nul:
|}{|\frac{a_nz^n}{2}|} = |\frac{P(z)}{\frac{a_nz^n}{2}}| = |2 + \sum \limits_{k=0}^{n-1} \frac{2a_k}{a_n}z^{k-n}|)
Certes, mais je peux faire quoi avec ça ?
J'y avais déjà pensé, mais je n'ai pas abouti
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 17:09
par Rha » 02 Fév 2014, 17:09
L'idée est qu'un polynôme est équivalent à son monôme de plus haut degré quand le module tend vers plus l'infini, parce que les autres termes sont négligeables devant celui de plus haut degré.
Dans la somme de droite, les exposants sont tous strictement négatifs, donc pour
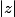
suffisamment grand, les

deviennent aussi petits qu'on veut.
Si tu as un cours sur la continuité et les limites, tu peux trancher la question un peu plus rapidement.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 17:18
par jonses » 02 Fév 2014, 17:18
Rha a écrit:L'idée est qu'un polynôme est équivalent à son monôme de plus haut degré quand le module tend vers plus l'infini, parce que les autres termes sont négligeables devant celui de plus haut degré.
Dans la somme de droite, les exposants sont tous strictement négatifs, donc pour
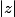
suffisamment grand, les

deviennent aussi petits qu'on veut.
Si tu as un cours sur la continuité et les limites, tu peux trancher la question un peu plus rapidement.
J'ai bien un cours sur la continuité et les limites, mais je n'ai rien concernant les fonctions de C dans C (j'ai juste les cours pour les fonctions de R dans R et de R dans C)
Là franchement je sais pas quoi faire, et même en essayant sur un exemple, je n'y arrive pas du tout
-
Doraki
- Habitué(e)
- Messages: 5021
- Enregistré le: 20 Aoû 2008, 11:07
-
 par Doraki » 02 Fév 2014, 17:27
par Doraki » 02 Fév 2014, 17:27
Tu n'as rien besoin de savoir à part l'inégalité triangulaire dans C : |a+b| <= |a| + |b|, plus divers autres trucs comme la compatibilité de l'ordre avec + et * dans R (si a <= b alors a+c <= b+c, et si c >= 0 alors ac <= bc)
En fait tu peux faire semblant que z est réel tout au long de l'histoire, ça devrait rien changer.
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 17:33
par jonses » 02 Fév 2014, 17:33
Doraki a écrit:Tu n'as rien besoin de savoir à part l'inégalité triangulaire dans C : |a+b| = 0 alors ac <= bc)
En fait tu peux faire semblant que z est réel tout au long de l'histoire, ça devrait rien changer.
Le problème c'est que j'y arrive pas du tout, avec les réels ou les complexes.
Je ne vois pas comment utiliser l'inégalité triangulaire dans cette affaire
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 17:37
par Rha » 02 Fév 2014, 17:37
Ok.
On passe au module alors: soient

deux complexes et

un réel strictement positif.
Si

.
De plus,

ce qui peut se généraliser à une somme finie.
Il ne reste plus qu'à montrer que si

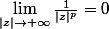
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 02 Fév 2014, 17:41
par jonses » 02 Fév 2014, 17:41
Rha a écrit:On passe au module alors: soient

deux complexes et

un réel strictement positif.
Si

.
Je suis d'accord, c'est d'ailleurs un résultat déjà acquis depuis un bon moment, mais je ne vois pas où ça peut me servir
Rha a écrit:Il ne reste plus qu'à montrer que si

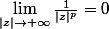
Même si je le montre, je ne suis pas sensé le savoir, ni l'utiliser d'ailleurs
-
Rha
- Membre Naturel
- Messages: 51
- Enregistré le: 21 Oct 2013, 22:35
-
 par Rha » 02 Fév 2014, 17:50
par Rha » 02 Fév 2014, 17:50
Le but de la méthode que j'ai proposée est de montrer que
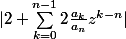
est plus grand que

si
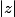
est de module suffisamment grand.
En utilisant ce qui précède, on voit qu'il suffit de montrer que
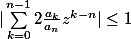
pour
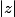
assez grand.
D'où la nécessité de contrôler les

, chose pour laquelle il suffit dans ce cas de contrôler leur module.
La limite dont je parle n'est pas vraiment hors du champ de connaissances requises, puisqu'elle concerne des modules, donc des réels.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 03 Fév 2014, 10:29
par Ben314 » 03 Fév 2014, 10:29
Salut,
Si tu as déjà vu les propriétés des limites lorsque |z|->oo (limite d'une somme, d'un produit, etc) alors ça ne prend que 2 lignes :
Du fait que
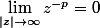
pour tout

on déduit que
}{z^n}=a_n)
et donc, par définition de la limite lorsque

, il existe
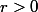
tel que
}{z^n}-a_n\right|r)
Or
}{z^n}-a_n\right|<\frac{|a_n|}{2}\ \Rightarrow\ |P(z)|\leq \frac{|a_n z^n|}{2})
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
jonses
- Membre Relatif
- Messages: 496
- Enregistré le: 19 Mai 2013, 09:33
-
 par jonses » 03 Fév 2014, 20:02
par jonses » 03 Fév 2014, 20:02
[quote="Ben314"]Salut,
Si tu as déjà vu les propriétés des limites lorsque |z|->oo (limite d'une somme, d'un produit, etc) alors ça ne prend que 2 lignes :
Du fait que
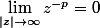
pour tout

on déduit que
}{z^n}=a_n)
et donc, par définition de la limite lorsque

, il existe
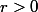
tel que
}{z^n}-a_n\right|r)
Or [TEX]\ \left|\frac{P(z)}{z^n}-a_n\right|oo"
Je pense que mon erreur vient du fait que j'ai confondu "quand z (complexe) tend vers ..." (chose que j'ai absolument pas vu, et qui ne m'a pas été définie) et " quand |z| (module qui est donc réel) tend vers..."
Mon explication est pas très rigoureuse, mais en bref, ce que je veux dire c'est que je n'ai pas saisi au début que je pouvais manipuler des limites de |z|
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
c'est immédiat.
, en utilisant la définition de la valeur absolue de réels:
, on a:
.
.
suffisamment grand, les
deviennent aussi petits qu'on veut.
deux complexes et
un réel strictement positif.
.
