Inégalité des accroissements finis

[wilfriedd]

Bonjour à tous,
voilà je vous présente l'exercice sur lequel je buche.
Montrer que l'équation f(x)=2 admet une solution unique a sur [0,2 ; 0,3], avec
f(x)=(x+1)e^(2x) et déterminer une valeur approchée de a à 10^(-5) près.
J'ai su faire cet exercice.
Pour la première partie j'ai utiliser le fait que f est strictement croissante et que f(0,2)<2J'aurai su aussi facilement faire par dichotomie la détermination de a à 10^(-5) près mais mon problème est le suivant (en fait cet exercice m'a été donné en préparation à l'oral 2 du CAPES) à la fin de l'exercice il est écrit:"exercice à mettre en forme avec le théorème des inégalités des accroissements finis"
J'essaye depuis un bout de temps déjà de trouver une valeur approchée de a grace à l'inégalité des accroissement fini mais je n'y arrive pas. Je pourrais le faire de proche en proche en réduisant l'intervalle dans lequel se trouve a mais je n'y voit pas d'interêt donc si quelqu'un pouvait m'aider.
Merci d'avance.

[mathelot]

Bonjour,

je ne sais si je suis hors sujet. En tous cas, voilà l'idée

on pose

il s'agit de calculer une valeur approchée
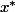
de la racine de l'équation




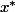
il y a plusieurs méthodes pour cela,de suites récurrentes convergeant vers , dont:

- la méthode de Newton

- la méthode de la "fausse position" (regula falsi)


la convergence de ces suites et la vitesse de convergence s'obtient avec ( une majoration de) Taylor-Lagrange.
Est-ce un énoncé de ce style qu'il est demandé de rédiger ?